Semiautomatic robust regression clustering of international trade data

Abstract

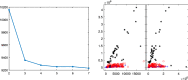
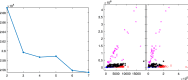
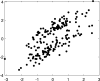
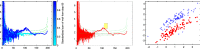
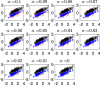
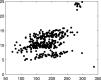
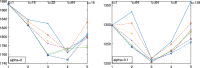
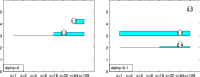
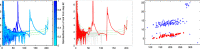
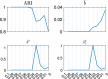
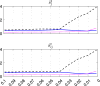
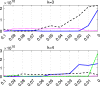
The purpose of this paper is to show in regression clustering how to choose the most relevant solutions, analyze their stability, and provide information about best combinations of optimal number of groups, restriction factor among the error variance across groups and level of trimming. The procedure is based on two steps. First we generalize the information criteria of constrained robust multivariate clustering to the case of clustering weighted models. Differently from the traditional approaches which are based on the choice of the best solution found minimizing an information criterion (i.e. BIC), we concentrate our attention on the so called optimal stable solutions. In the second step, using the monitoring approach, we select the best value of the trimming factor. Finally, we validate the solution using a confirmatory forward search approach. A motivating example based on a novel dataset concerning the European Union trade of face masks shows the limitations of the current existing procedures. The suggested approach is initially applied to a set of well known datasets in the literature of robust regression clustering. Then, we focus our attention on a set of international trade datasets and we provide a novel informative way of updating the subset in the random start approach. The Supplementary material, in the spirit of the Special Issue, deepens the analysis of trade data and compares the suggested approach with the existing ones available in the literature.

Keywords: Clustering; Forward search; International trade; Monitoring; Multiple start; Outliers; Regression; TCLUST; Trimming.

Fig. 1

352 imports of FFP2 and FFP3 masks (product 6307909810) into the European Union extracted in a day of November. Vertical axes: traded value, horizontal axes: traded weight (W) and number of units (SU). The point highlighted with an arrow in the left panel is a typical case of a unit which is far from each possible group

Fig. 2

FFP3 and FFP4 imports in November 2020: Flexible Mixture Modeling BIC (left panel) and classification based on $k=4$ (right panel)

Fig. 3

FFP3 and FFP4 imports in November 2020: flexible cluster-weighted modeling BIC (left panel) and classification (right panel)

Fig. 4

Dataset X: scatterplot

Fig. 5

Dataset X: identification of the best number of groups k and restriction factor c with the elbow plot (on the horizontal axis k) and the car-bike plot (on the vertical axis k)

Fig. 6

Dataset X: step 1 of iterative FS-based random start approach (the three panels represent respectively steps a/b/c of the iterative approach)

Fig. 7

Dataset X: step 2 of iterative FS-based random start approach (the three panels 1/2/3 represent respectively step a/b/c of the iterative approach)

Fig. 8

Dataset X: estimation of the best trimming level $\alpha$ (given $k=2$ and $c=1$, identified in Figs. 4, 5, 6 and 7). For 11 values of the trimming level $\alpha$ ranging in the interval [0, 0.1], monitoring of changes in: (i) Adjusted Rand Index, (ii) regression coefficients $\widehat{b}$ (iii) biased variance (${\widehat{s}}^2$), (iv) unbiased error variance (${\widehat{s}}_c^2$)

Fig. 9

Dataset X: estimation of the best trimming level $\alpha$ (for $k=2$ and $c=1$, identified in Figs. 4, 5, 6 and 7). For 11 values of the trimming level $\alpha$ ranging in the interval [0, 0.1], monitoring for each group (i) error variances (${\widehat{s}}_j^2$), (ii) unbiased error variances (${\widehat{s}}_{\mathit{cj}}^2$)

Fig. 10

Dataset X: estimation of the best trimming level $\alpha$ (given $k=2$ and $c=1$, identified in Figs. 4, 5, 6 and 7). For 11 values of the trimming level $\alpha$ ranging in the interval [0, 0.1], monitoring: 1st panel: units changing classification; 2nd panel: posterior probabilities of each unit; 3rd panel: scatter of the k groups with the $11\times k$ regression lines

Fig. 11

Dataset X: estimation of the best trimming level $\alpha$ (given $k=2$ and $c=1$, identified in Figs. 4, 5, 6 and 7). For 11 values of the trimming level $\alpha$ ranging in the interval [0, 0.1], monitoring the scatter of y vs X with allocation for each of the 11 values of $\alpha$

Fig. 12

Pinus dataset: height (y axis, in meters) and diameter (x axis, in millimeters) of 362 Pinus nigra trees located in the north of Palencia (Spain)

Fig. 13

Pinus dataset: elbow plot (on the horizontal axis k) obtained for $\alpha =0$ and $\alpha =0.1$ respectively

Fig. 14

Pinus dataset: car-bike plot (on the vertical axis k) obtained for $\alpha =0$ and $\alpha =0.1$ respectively

Fig. 15

Pinus dataset: cluster identified by brushing the minimum deletion residual plot computed on all observations

Fig. 16

Pinus dataset: cluster identified by brushing the minimum deletion residual plot computed on all observations after having excluded the cluster identified in Fig. 15

Fig. 17

Pinus dataset: cluster identified by brushing the minimum deletion residual plot computed on all observations after having excluded the clusters identified in Figs. 15 and 16

Fig. 18

Pinus dataset: estimation of the best trimming level $\alpha$ (given $k=3$ and $c=8$, identified in Figs. 13, 14, 15, 16 and 17). For 11 values of the trimming level $\alpha$ ranging in the interval [0, 0.1], monitoring of the changes in (i) Adjusted Rand Index , (ii) regression coefficients $\widehat{\beta }$, (iii) error variance (${\widehat{s}}^2$), (iv) corrected error variance (${\widehat{s}}_c^2$)

Fig. 19

Pinus dataset: estimation of the best trimming level $\alpha$ (given $k=3$ and $c=8$, identified in Figs. 13, 14, 15, 16 and 17). For 11 values of the trimming level $\alpha$ ranging in the interval [0, 0.1], monitoring for each group (i) error variances (${\widehat{s}}_j^2$), (ii) unbiased error variances (${\widehat{s}}_{\mathit{cj}}^2$)

Fig. 20

Pinus dataset: estimation of the best trimming level $\alpha$ (given $k=3$ and $c=8$ identified in Figs. 13, 14, 15, 16 and 17). For 11 values of the trimming level $\alpha$ ranging in the interval [0, 0.1], monitoring of the: 1st panel: units changing classification; 2nd panel: posterior probabilities of each unit. 3rd panel: scatter of the k groups with the $11·k$ regression lines

Fig. 21

Pinus dataset: estimation of the best trimming level $\alpha$ (given $k=3$ and $c=8$ identified in Figs. 13, 14, 15, 16 and 17). For 11 values of the trimming level $\alpha$ ranging in the interval [0, 0.1], monitoring of the scatter of y against X with allocation for the 11 values of $\alpha$ ranging in the interval [0, 0.1]

Fig. 22

Face masks data: elbow plot (k on the horizontal axis) and car-bike plot (k on the vertical axis)

Fig. 23

Face masks data: monitoring of error variances when $k=3$ (top panel) and $k=4$ (bottom panel)

Fig. 24

Face mask data: final classification based on $k=3$; the $4\%$ trimmed units (denoted in the legend with symbol ‘+’ -1 in faint grey) are not shown

Fig. 25

Face mask data: final classification based on $k=4$; the $3\%$ trimmed units (denoted in the legend with symbol ‘+’ -1 in faint grey) are not shown

Fig. 26

Real trade data. First panel: 153 imports of girdles and panty girdles (product code 6212.20.00.00 in the combined international nomenclature) from a given third country to a specific Member State. Second panel: 1702 imports of toothed wheels, chain sprockets and other transmission elements (product code 8483.90.89.90 in the combined international nomenclature) from a given third country to a specific Member State

Fig. 27

Simulated trade like data where the X variable is simulated from a Uniform (1st panel) and from a Tweedie (2nd panel)