Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019;15(12):10.1038/s41567-019-0670-x.
doi: 10.1038/s41567-019-0670-x.

Extreme magnetic field-boosted superconductivity

Sheng Ran  1   2   3 , I-Lin Liu  1   2   3 , Yun Suk Eo  1 , Daniel J Campbell  1 , Paul M Neves  1 , Wesley T Fuhrman  1 , Shanta R Saha  1   2 , Christopher Eckberg  1 , Hyunsoo Kim  1 , David Graf  4 , Fedor Balakirev  5 , John Singleton  5   6 , Johnpierre Paglione  1   2 , Nicholas P Butch  1   2
Affiliations

Extreme magnetic field-boosted superconductivity

Sheng Ran et al. Nat Phys. 2019.

Abstract

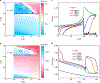
Applied magnetic fields underlie exotic quantum states, such as the fractional quantum Hall effect1 and Bose-Einstein condensation of spin excitations2. Superconductivity, however, is inherently antagonistic towards magnetic fields. Only in rare cases3-5 can these effects be mitigated over limited fields, leading to re-entrant superconductivity. Here, we report the coexistence of multiple high-field re-entrant superconducting phases in the spin-triplet superconductor UTe2 (ref. 6). We observe superconductivity in the highest magnetic field range identified for any re-entrant superconductor, beyond 65 T. Although the stability of superconductivity in these high magnetic fields challenges current theoretical models, these extreme properties seem to reflect a new kind of exotic superconductivity rooted in magnetic fluctuations7 and boosted by a quantum dimensional crossover8.

PubMed Disclaimer

Conflict of interest statement

Competing interests The authors declare no competing interests.

Figures

Fig. 1 |
Fig. 1 |. Magnetic field-induced superconducting and polarized phases of uTe2.
a, Sketch of how the magnetic field is applied with respect to the three crystallographic axes of UTe2. b, Top view of the sample platform with a two-axis rotator used in d.c. field measurements to achieve the best alignment. c, Magnetic field–angle phase diagram showing the three superconducting phases SCPM, SCRE and SCFP. FP is the field-polarized phase. The magnetic field is rotated within the a–b and b–c planes. The critical field values of the SCPM and SCRE phases are based on d.c. field measurements, and those of the SCFP and FP phases are based on pulsed field measurements. The SCRE phase was not observed for angles of θ larger than 3.9° in the b–c plane (Supplementary Fig. 1). The dashed lines are guides to the eye.
Fig. 2 |
Fig. 2 |. Re-entrance of superconductivity in uTe2.
a, Field dependence of R in UTe2 at T = 0.35 K measured in the d.c. field. The magnetic field is rotated from the b axis towards the a axis. Zero resistance persists up to 34.5 T when the magnetic field is perfectly along the b axis. The same dataset is plotted on a logarithmic scale in the inset. Re-entrance of superconductivity can be clearly seen when the magnetic field is applied slightly off the b axis. b, Magnetoresistance R and f of the PDO circuit (see Methods for technical details) in UTe2 at T = 0.45 K in the pulsed field, with the magnetic field applied along the b axis. c, Magnetization measurements of UTe2 at T = 0.46 K and 1.69 K in the pulsed field, with the magnetic field applied along the b axis. The two-axis rotator is not compatible with measurements in the pulsed field. There is probably a slight angle offset along the perpendicular direction. SCRE is not observed in these measurements. f.u., formula unit.
Fig. 3 |
Fig. 3 |. angle dependence of the field-induced superconducting and polarized phases of uTe2.
a–c, When the magnetic field is applied at an angle from the b axis towards the c axis (or a axis), it is equivalent to two applied magnetic fields: one along the b axis, Hb = Hcosθ or Hcosϕ, and the other along the c axis, Hc = Hsinθ (or along the a axis, Ha = Hsinϕ). Colour contour plots are shown for magnetoresistance R as a function of Hc and Hb (a), f of the PDO circuit as a function of Hc and Hb (b), and magnetoresistance R as a function of Ha and Hb (c). The blue dots are the critical fields for the field-polarized state and the red dots are the critical fields for SCFP. The dotted lines in a and b indicate the directions along which measurements were also performed at different temperatures, as shown in Fig. 4. d–f, The corresponding data as a function of the applied magnetic fields at selected angles.
Fig. 4 |
Fig. 4 |. Temperature dependence of SCFP in uTe2.
a,b, Colour contour plots of R (a) and f (b) of PDO measurements as a function of T and H at θ = 23.7° (a) and θ = 33° (b). The blue dots are the critical fields for SCFP and the dashed lines are guides to the eye, extrapolated to the region where there are no data. c,d, The corresponding data as a function of the applied magnetic fields at selected temperatures.
See this image and copyright information in PMC

References

    1. Stormer HL Nobel lecture: the fractional quantum Hall effect. Rev. Mod. Phys 71, 875–889 (1999).
    1. Zapf V, Jaime M & Batista CD Bose–Einstein condensation in quantum magnets. Rev. Mod. Phys 86, 563–614 (2014).
    1. Meul HW et al. Observation of magnetic-field-induced superconductivity. Phys. Rev. Lett 53, 497–500 (1984).
    1. Uji S et al. Magnetic-field-induced superconductivity in a two-dimensional organic conductor. Nature 410, 908–910 (2001). - PubMed
    1. Konoike T et al. Magnetic-field-induced superconductivity in the antiferromagnetic organic superconductor κ-(BETS)2FeBr4. Phys. Rev. B 70, 094514 (2004).