Guidestar-free image-guided wavefront shaping

Abstract

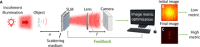
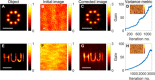
Optical imaging through scattering media is a fundamental challenge in many applications. Recently, breakthroughs such as imaging through biological tissues and looking around corners have been obtained via wavefront-shaping approaches. However, these require an implanted guidestar for determining the wavefront correction, controlled coherent illumination, and most often raster scanning of the shaped focus. Alternative novel computational approaches that exploit speckle correlations avoid guidestars and wavefront control but are limited to small two-dimensional objects contained within the "memory-effect" correlation range. Here, we present a new concept, image-guided wavefront shaping, allowing widefield noninvasive, guidestar-free, incoherent imaging through highly scattering layers, without illumination control. The wavefront correction is found even for objects that are larger than the memory-effect range, by blindly optimizing image quality metrics. We demonstrate imaging of extended objects through highly scattering layers and multicore fibers, paving the way for noninvasive imaging in various applications, from microscopy to endoscopy.

Fig. 1. Noninvasive imaging via image-guided wavefront shaping, concept, and numerical results.

(A) An incoherently illuminated object is hidden behind a highly scattering medium. The scattered light wavefront is shaped by a high-resolution SLM, which is conjugated to the scattering medium surface. The wavefront-shaped light is Fourier-transformed by a lens on a high-resolution camera. (B) The initial camera image is a low-contrast diffusive blur. (C) Image-guided iterative optimization of the SLM phase correction aimed at maximizing a quality metric of the captured image yields a wavefront correction with ~10⁴ DOFs and a sharp, high-contrast widefield image of the hidden object.

Fig. 2. Comparison of basic image quality metrics and description of the wavefront optimization process.

(A to C) 1D examples for imaging a simple two-point object using the following: (A) the initial uncorrected speckle PSF, (B) the desired wavefront-corrected diffraction-limited PSF, and (C) an undesired matched-filter PSF that resembles the object structure, which yields the same peak intensity in the camera image as the desired diffraction-limited PSF but does not recover the object. A desired image quality metric must distinguish between the two PSFs of (B) and (C). (D) Comparison of three basic metrics for the simulated cases of (A) to (C): peak intensity, image variance (“var”), and modified entropy (“H”; see section S3). The variance and entropy successfully distinguish the desired PSF of (C) from the undesired one of (B). (E to G) The proposed two-step wavefront optimization process: (E) initial uncorrected camera image for a flat-phase SLM. (F) As a first step, the SLM wavefront correction is optimized to minimize the modified entropy of the camera image. This results in partial correction with a few replications of the object, from which a small ROI (dashed line) for the second optimization step is extracted. (G) Variance maximization on the extracted ROI results in wavefront correction and high-resolution imaging.

Fig. 3. Experimental imaging through a single highly scattering layer.

(A) The object as imaged directly without the scattering layer. (B) The initial image through a highly scattering thin diffuser (60° scattering angle). (C) Camera image after image-guided wavefront optimization. (D) Evolution of the variance metric gain as a function of the optimization iterations. (E to H) Same as (A) to (D) for a different object and 20° diffuser. Scale bars, (A to C) 2 mm and (E to G) 1.5 mm.

Fig. 4. Imaging extended objects through volumetric scattering with a limited memory effect.

(A to D) Numerical results for the case of an object whose top and bottom halves are scattered by uncorrelated scattering functions. (A) The hidden object. (B) Initial camera image with uncorrected wavefront. (C and D) Final results of camera images from two independent optimizations, each randomly converges to a different wavefront correction matching a single isoplanatic patch (memory-effect FoV). (E to H) Experimental results through a scattering medium composed of two diffusers. (E) Object as imaged without scattering. (F) Camera image before correction. (G) Camera image after image-guided optimization corrects the left half of the object. (H) Final SLM phase pattern after optimization. Scale bars, (A to D) 1.1 mm and (E to G) 1.5 mm.

Fig. 5. Lensless widefield endoscopic imaging through an MCF bundle.

(A) Schematic of the experiment: An incoherently illuminated object is placed at a small distance from the distal facet of an MCF bundle having thousands of cores. The fiber proximal facet is conjugated to the SLM (4-f imaging telescope omitted for simplicity) and Fourier-transformed on a camera. (B) The object: USAF target group 5 elements 3 to 5 placed 3.8 mm from the fiber bundle. (C) Conventional image of the fiber proximal facet does not reveal any object features. (D) The initial camera image without correction. (E) The final image after image-guided wavefront optimization, correcting both the intracore phase distortions and defocus, resulting in a diffraction-limited image of the object. Scale bars, 100 μm. See movie S1 for the evolution of the image correction. au, arbitrary units.