DotMotif: an open-source tool for connectome subgraph isomorphism search and graph queries

Abstract

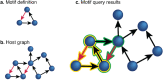
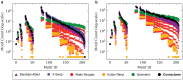
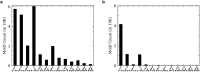
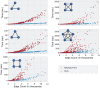
Recent advances in neuroscience have enabled the exploration of brain structure at the level of individual synaptic connections. These connectomics datasets continue to grow in size and complexity; methods to search for and identify interesting graph patterns offer a promising approach to quickly reduce data dimensionality and enable discovery. These graphs are often too large to be analyzed manually, presenting significant barriers to searching for structure and testing hypotheses. We combine graph database and analysis libraries with an easy-to-use neuroscience grammar suitable for rapidly constructing queries and searching for subgraphs and patterns of interest. Our approach abstracts many of the computer science and graph theory challenges associated with nanoscale brain network analysis and allows scientists to quickly conduct research at scale. We demonstrate the utility of these tools by searching for motifs on simulated data and real public connectomics datasets, and we share simple and complex structures relevant to the neuroscience community. We contextualize our findings and provide case studies and software to motivate future neuroscience exploration.

Figure 1

Subgraph search. Subgraph search is formally defined in “Background” section. (a) A motif query is defined. In this example, the query is a simple directed triangle. One edge (red) has been assigned an attribute constraint (perhaps a neurotransmitter type or weight threshold). (b) A directed search graph, or “host” graph. Two edges in the host graph share the same attribute as the constrained edge in the motif. (c) The motif is discovered in the search graph. Two unique detections are shown here, highlighted in yellow and green. Note that edges and nodes in the host graph may appear in more than one mapping.

Figure 2

A comparison of DotMotif query syntax and the equivalent queries when transpiled to Cypher using the Neo4jExecutor. (a) A simple query to find inputs to Kenyon cells (KC) from the medial antennal lobe tracts (mALT) in the Hemibrain dataset. Note that DotMotif comments are notated with the hash character. (b) The equivalent query as panel (a), when converted to the Cypher query language for use with neuPrint systems. Even in a small query such as this, DotMotif syntax tends to be more succinct and readable. (c) A simple DotMotif query for a repeated pattern with node and edge constraints. The motif includes a macro called BigInhibitsSmall, which establishes a connection between two neurons with a type edge-attribute of “GABA”, and with radius nodes attribute constraints on both neuron participants. This macro is reused multiple times in the final motif construction in order to avoid repetitive code. DotMotif automatically infers that nodes A and B are isomorphic (i.e. interchangeable), and that C and D are isomorphic. (d) DotMotif converts the query in panel (c) to the Cypher code in (d). The equivalent Cypher query is substantially longer and harder to maintain or edit, even in the case of this quite simple motif. It also requires explicit notation to avoid reporting duplicate motif automorphisms.

Figure 3

Undirected motif searches (monomorphisms) in connectomes and random graphs. (a,b) The count of every undirected subgraph with six or fewer vertices ($|V|\le 6$). Each motif was counted in the connectomes, as well as in each of the random graph models calibrated to match the density of each connectome. The x-axis is the motif ID from the Atlas of Graphs text (e.g. all points on the line $x=7$ represent the undirected triangle motif). Gaps along the x-axis indicate omitted motifs (i.e., those with multiple connected components). (a) Comparing C. elegans with random graphs calibrated to C. elegans density. Due to its higher density, the C. elegans graph has higher motif counts than those of the MICrONS graph, despite a lower vertex count. X-swap motif counts (blue) closely match those of the original connectome (black). In contrast, Erdős–Rényi approximations (yellow) are very poor predictors of true connectome motif count, and always under-estimate motif counts in the original connectome. The parameter-space of the Watts–Strogatz model (red) leads to a wide range of motif count predictions, some as low as those of the Erdős–Rényi model. (b) Comparing MICrONS with random graphs calibrated to MICrONS density. Like the C. elegans results in (a), Erdős–Rényi approximations always underestimate the number of motifs, for all motif graphs we searched. The same motifs ($x=77$, $x=78$, etc) occur with the highest frequency in the MICrONS graph as in the C. elegans graph. Motif $x=208$, the fully-connected graph on six nodes, appears many thousands of times in the C. elegans graph, but does not occur at all in the MICrONS connectome. Some models, like X-swap and Erdős–Rényi, likewise predict zero $K_6$ motif occurrences. Others, like the geometric model (green), erroneously overpredict the number of expected $K_6$ subgraphs. Full-resolution copies of this graphic are available online (see Supplemental Material 1).

Figure 4

Quantities (monomorphisms) of directed three-node motifs from the C. elegans chemical synapse connectome and the MICrONS v185 graph. (a) C. elegans directed three-node motif counts. The most commonly encountered directed three-node motif is the “fan-in” motif, where two neurons converge to a single downstream target. All directed three-node motifs occur at least once. (b) MICrONS v185 directed three-node motif counts. The most common motif is the “fan-out” motif, where one neuron synapses onto two downstream targets. Several three-node motifs appear infrequently or do not appear at all. This illustrates differences between the connectivity patterns of a complete connectome such as the worm’s and a mammalian brain region that is expected to be largely feed-forward.

Figure 5

Comparison of wall-clock runtime when counting undirected motifs. All runtimes are measured during motif searches in Erdős–Rényi graphs with node-count sampled uniformly on the interval of 100–300 nodes, and with densities randomly sampled between 0 and 0.3. See Benchmarks for more details. Here, we compare performance on a variety of motifs, such as the three-node path graph, the four-node cycle graph, and complete cliques of various sizes.

Figure 6

The DotMotif query execution process. Graph import. A user may import a search graph (also commonly referred to as a host graph) from a variety of industry standard formats, including an edgelist CSV, GraphML, numpy adjacency matrix, and any format supported by the NetworkX library. Furthermore, DotMotif is compatible with graphs stored in neuPrint schemas in a Neo4j database. Query design. The user may select from a library of pre-built motifs, or write a novel query. The query may be written in the DotMotif DSL, encoded as a NetworkX graph, or written as text directly in the target graph database query language, such as Cypher. A user may choose to save this query as another standalone file on disk for future use. The .motif file-format stores both the motif itself and provenance metadata such as the date of creation, comments associated with the motif, and author information. Query validation. DotMotif supports several pre-execution validation steps in order to fail quickly when asked to perform an impossible or self-contradictory query. Several other optional validators may be invoked to check a motif for biological feasibility and to warn the user if a potential error is detected. Execution and results. The user may choose from the available DotMotif Executors in order to use the most appropriate subgraph matching tool for the compute resources available. No further query modification is required in order to run the same motif on several different Executors. A user may also choose to simply use DotMotif as a query executor without leveraging the query validation or query design tools.

Figure 7

Examples of the DotMotif query language. (a) Features of the DotMotif domain-specific language syntax. Nodes are connected by directed edges, notated with an arrow operator. A user can specify whether a certain edge must not exist by using the non-edge operator. Both edges as well as nodes may be assigned constraints or attributes. Edge attributes are nested in square brackets on the same line as the edge notation, and node attributes are notated with ‘dot’ notation on their own line. A user can explicitly indicate that two nodes are interchangeable, and DotMotif will only return one representative of that automorphism group. (b) Example use of nested macros to construct a complex motif from simple building blocks. In this motif example, x, y, and z serve as macro arguments. These variables, similar to local function arguments in other programming languages, are only used within the macro, and are not participants in the motif. Nodes with names A–E serve as participants in the motif. Note that macros may be nested by calling one from within the body of another. (c) Examples of motifs that fail validation. The DotMotif query validation step reduces the likelihood of spending computational resources on impossible or biologically unfeasible queries. In the first example, validation fails because an edge has already been added to the motif but a new line (red underline) conflicts with this requirement. In the second example, validation fails because the condition is impossible (no value for A.size can be both greater than 50 as well as less than or equal to 5). These validation failures serve as early warning-signs for a researcher to see that a query will fail if executed.

Figure 8

The DotMotif Syntax in railroad-diagram form. The DotMotif DSL is a whitespace-agnostic language with hash-symbol comments and curly-brace bracketed macros. Edges are defined with ->-arrowlike syntax; edge attributes may be listed in JSON-like syntax. Node attributes may be listed in object dot-notation syntax. For example usage of this syntax system, refer to Architecture. This syntax is formally defined in Extended Backus-Naur Form. Both this formal definition as well as the language specification will be made available as per Supplemental Material 1. This figure was generated with the railroad-diagrams Node.js package.