One for all: Universal material model based on minimal state-space neural networks

Abstract

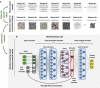
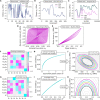
Computational models describing the mechanical behavior of materials are indispensable when optimizing the stiffness and strength of structures. The use of state-of-the-art models is often limited in engineering practice due to their mathematical complexity, with each material class requiring its own distinct formulation. Here, we develop a recurrent neural network framework for material modeling by introducing "Minimal State Cells." The framework is successfully applied to datasets representing four distinct classes of materials. It reproduces the three-dimensional stress-strain responses for arbitrary loading paths accurately and replicates the state space of conventional models. The final result is a universal model that is flexible enough to capture the mechanical behavior of any engineering material while providing an interpretable representation of their state.

Fig. 1. Mechanical material modeling workflow.

(A) Examples of classes of engineering materials (middle) each requiring a different model (top) and implementation when taking the conventional physics-based modeling approach. A single universal model (bottom) replaces the different models when adopting a machine learning–based systematic solution. (B) Information flow in an MSC with three inputs and three outputs, n_s = 2, w = 5, d_t = 2, and d_o = 1. Each weighted connection (thin line) represents a parameter of the model. Bias terms are not represented. Symbols ψ and φ, respectively, represent the hyperbolic tangent and logistic sigmoid activation functions.

Fig. 2. Effect of model architecture on the performance of MSCs.

(A to D) Effect of the number of state variables n_s of MSCs, with comparison (A and B) to single-layer GRUs and LSTMs. (A) Isotropic-hardening model (7 state variables). (B) Mixed-hardening model (12 state variables). (C) Foam model (7 state variables). (D) Rubber model (7 state variables). (E and F) Effect of the number of parameters on the mean squared error on the validation datasets for optimal state-space MSCs compared with stacked LSTMs and GRUs for the (E) isotropic-hardening model and (F) mixed-hardening model.

Fig. 3. Predictive capabilities of MSCs and learned features for different materials.

Results for compact MSC models (with d_t = 4 and w = 25) after training with random walk data compared to Finite Element Model (FEM) results. (A to C) First stress component prediction on the worst predicted example for the mixed-hardening material: (A) validation dataset, (B) 500-long test dataset, and (C) 100,000-long test dataset. (D) Bauschinger effect for cyclic loading of the mixed-hardening material. (E) Mullins effect during unloading-reloading of the rubber material. (F and G) Spearman correlation coefficients between state variables of MSCs and state variables of the physics-based models evaluated on the validation dataset of (F) the isotropic-hardening model and (G) the crushable foam model. (H and I) Internal state variable of an MSC model as a function of the equivalent plastic strain of the corresponding physics-based model for the 500 validation examples for the (H) isotropic-hardening model and (I) crushable foam model. (J and K) Extraction of yield surface and demonstration of their self-similar evolution by plotting iso-contours of the MSC-inferred internal state variable. Gray lines indicate the isolines of the theoretical yield surface for comparison. (J) Iso-levels (0.0001, 0.01, 0.02, 0.03, 0.04, and 0.05) obtained from 3000 isochoric proportional loading path simulations for the isotropic-hardening model. (K) Iso-levels (0.003, 0.03, 0.06, 0.09, 0.12, and 0.15) obtained from 1000 proportional loading path simulations for the crushable foam model.