Memristor Circuits for Simulating Neuron Spiking and Burst Phenomena

Abstract

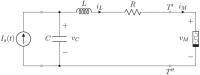
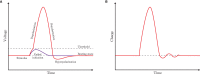
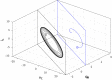
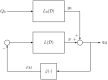
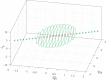
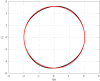
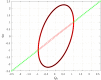
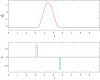
Since the introduction of memristors, it has been widely recognized that they can be successfully employed as synapses in neuromorphic circuits. This paper focuses on showing that memristor circuits can be also used for mimicking some features of the dynamics exhibited by neurons in response to an external stimulus. The proposed approach relies on exploiting multistability of memristor circuits, i.e., the coexistence of infinitely many attractors, and employing a suitable pulse-programmed input for switching among the different attractors. Specifically, it is first shown that a circuit composed of a resistor, an inductor, a capacitor and an ideal charge-controlled memristor displays infinitely many stable equilibrium points and limit cycles, each one pertaining to a planar invariant manifold. Moreover, each limit cycle is approximated via a first-order periodic approximation analytically obtained via the Describing Function (DF) method, a well-known technique in the Harmonic Balance (HB) context. Then, it is shown that the memristor charge is capable to mimic some simplified models of the neuron response when an external independent pulse-programmed current source is introduced in the circuit. The memristor charge behavior is generated via the concatenation of convergent and oscillatory behaviors which are obtained by switching between equilibrium points and limit cycles via a properly designed pulse timing of the current source. The design procedure takes also into account some relationships between the pulse features and the circuit parameters which are derived exploiting the analytic approximation of the limit cycles obtained via the DF method.

Keywords: bursting; harmonic balance; memristor; neuron; pulse-programmed circuit; spiking.

Figure 1

Charge-controlled memristor circuit with R, L,C components and independent current source I_s.

Figure 2

(A) Schematic of an ideal voltage-pulse of the cellular membrane (action potential). (B) Reference shape of the memristor charge-pulse considered in this paper. For the sake of simplicity, the depolarization is assumed to occur without distinction between the sub- and the super-threshold branches, and the hyperpolarization dynamics admits small ripples during the convergence to the resting state.

Figure 3

Invariant manifolds of the input-less circuit: the state space trajectory generated by the solution of Equation (3) with initial conditions v_C(t₀), q_M(t₀), i_L(t₀) (marked with ◦) at time t = t₀ belongs to the manifold M(Q₀) with Q₀ = q_M(t₀) + Cv_C(t₀) for all t ≥ t₀.

Figure 4

Stable (green half lines) and unstable (red segment) equilibrium points: the trajectories starting on the planes with $Q_0<-{\stackrel{-}{Q}}_0$ and $Q_0>{\stackrel{-}{Q}}_0$ converge toward the corresponding equilibrium points; the trajectory starting on the plane with $Q_0\in (-{\stackrel{-}{Q}}_0,{\stackrel{-}{Q}}_0)$ converges toward the stable limit cycle (green).

Figure 5

Equivalent input-output representation of system (7).

Figure 6

Input-less circuit attractors: stable (green ⋆) equilibrium points and stable PLCs (solid green) given by Equations (27) and (28) as a function of the manifold index Q₀. The red circles denote the unstable equilibrium points.

Figure 7

True limit cycle (solid dark) and PLC (solid red) in the (q_M, i_L)-plane for Q₀ = 0.

Figure 8

Stable (green ⋆) and unstable (red ◦) equilibrium points; maximum (32) and minimum (31) of the PLCs (solid red) as a function of Q₀; maximum and minimum values of the numerically computed limit cycles (dotted dark points).

Figure 9

Dynamics generated by applying at t_i = 10 a rectangular pulse of area Λ and width Δ = 1 via the current source I_s; the circuit parameters are as in Equation (30) and the initial conditions are q_M(0) = −2 and I_L(0) = 0, while Q(0) = −2. (A) For Λ = 0.5, the index Q(t) and the state variables q_M(t), i_L(t) converge to Q₀ = −1.5 and to the equilibrium point (−1.5, 0), respectively. (B) For Λ = 2.5, Q(t) converges to Q₀ = 0.5 and the state variables q_M(t), i_L(t) converge to the limit cycle belonging to the manifold M(0.5).

Figure 10

Top: predicted behavior $q_M^0(t)$ of the memristor charge. Bottom: timing of the current pulses.

Figure 11

The set pulse is applied at t_i = 2 with area A = 1.7889 and width Δ = 0.0487, the reset pulse is applied at t_i + Δ + T = 4.4821 with area Λ = −1.7889 and width Δ = 0.0487. The initial conditions are Q(0) = −2.2361, q_M(0) = −2.2361 and i_L(0) = 0. (A) Time behaviors of q_M (blu) and $q_M^0$ (red). (B) Trajectories in the state space generated by (Q(t), q_M(t), i_L(t)) (blu) and $(Q(t),q_M^0(t),i_L^0(t))$ (red).

Figure 12

The initial conditions are as in Figure 11, the set pulses are activated at t_i ∈ {10, 60, 110} and the reset pulses are applied 19.5164 time units later. (A) Time behavior of q_M for n = 8. (B) Time behavior of I_s.