Neuronal Graphs: A Graph Theory Primer for Microscopic, Functional Networks of Neurons Recorded by Calcium Imaging
- PMID: 34177469
- PMCID: PMC8222695
- DOI: 10.3389/fncir.2021.662882
Neuronal Graphs: A Graph Theory Primer for Microscopic, Functional Networks of Neurons Recorded by Calcium Imaging
Abstract
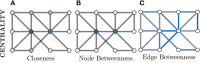
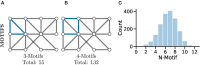
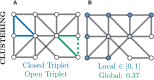
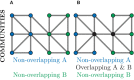
Connected networks are a fundamental structure of neurobiology. Understanding these networks will help us elucidate the neural mechanisms of computation. Mathematically speaking these networks are "graphs"-structures containing objects that are connected. In neuroscience, the objects could be regions of the brain, e.g., fMRI data, or be individual neurons, e.g., calcium imaging with fluorescence microscopy. The formal study of graphs, graph theory, can provide neuroscientists with a large bank of algorithms for exploring networks. Graph theory has already been applied in a variety of ways to fMRI data but, more recently, has begun to be applied at the scales of neurons, e.g., from functional calcium imaging. In this primer we explain the basics of graph theory and relate them to features of microscopic functional networks of neurons from calcium imaging-neuronal graphs. We explore recent examples of graph theory applied to calcium imaging and we highlight some areas where researchers new to the field could go awry.
Keywords: brain networks; calcium imaging; functional connectivity; graph theory; network analysis; neuronal networks.
Copyright © 2021 Nelson and Bonner.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures





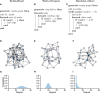
References
-
- Albert R., Barabási A.-L. (2002). Statistical mechanics of complex networks. Rev. Modern Phys. 74, 47–97. 10.1103/RevModPhys.74.47 - DOI
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

