Load Distribution in the Lumbar Spine During Modeled Compression Depends on Lordosis

Abstract

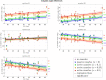
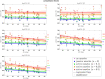
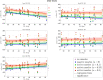
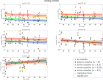
Excessive or incorrect loading of lumbar spinal structures is commonly assumed as one of the factors to accelerate degenerative processes, which may lead to lower back pain. Accordingly, the mechanics of the spine under medical conditions, such as scoliosis or spondylolisthesis, is well-investigated. Treatments via both conventional therapy and surgical methods alike aim at restoring a "healthy" (or at least pain-free) load distribution. Yet, surprisingly little is known about the inter-subject variability of load bearings within a "healthy" lumbar spine. Hence, we utilized computer tomography data from 28 trauma-room patients, whose lumbar spines showed no visible sign of degeneration, to construct simplified multi-body simulation models. The subject-specific geometries, measured by the corresponding lumbar lordosis (LL) between the endplates of vertebra L1 and the sacrum, served as ceteris paribus condition in a standardized forward dynamic compression procedure. Further, the influence of stimulating muscles from the M. multifidus group was assessed. For the range of available LL from 28 to 66°, changes in compressive and shear forces, bending moments, as well as facet joint forces between adjacent vertebrae were calculated. While compressive forces tended to decrease with increasing LL, facet forces were tendentiously increasing. Shear forces decreased between more cranial vertebrae and increased between more caudal ones, while bending moments remained constant. Our results suggest that there exist significant, LL-dependent variations in the loading of "healthy" spinal structures, which should be considered when striving for individually appropriate therapeutic measures.

Keywords: Cobb angle; MBS model; biomechanics; curvature; forward dynamics; lumbar lordosis; musculo skeletal model.

Figure 1

(A) CT image of the lumbar spine, rotated to standing position. (B) Computer model based on the subject-specific CT geometries, including passive structures [intervertebral disks (IVDs), facet joints and ligaments]. (C,D) In a last step, active force elements, muscles, are inserted into the model according to individual landmarks. The pelvis serves as origin for the M. psoas major group.

Figure 2

Examples of lumbar spinal curvature: (A) hypolordotic (LL = 28°), (B) regular (LL = 49.2°), and (C) hyperlordotic (LL = 66.3°). The method of calculating the LL, the sacral slope (SS), and the pelvic incident (PI) is sketched in (D) and described in the text. A vertical force of 500 N (blue arrows with dashed line of action) was applied on the COM of the vertebral body of L1 in all models.

Figure 3

PI, SS, and ΔPILL plotted against LL. The blue circles represent the PI, orange asterisks the SS, and black squares the ΔPILL for the 28 individual lumbar spines. Regressions lines (with confidence bands) are displayed in corresponding colors and their equations as well as coefficients of determination (R²) are stated in the annotations.

Figure 4

Differences in Cobb angles during compression of all 28 vertebrae against LL. Colors and marker symbols of the data points and the corresponding regression lines consistently correspond to the modes: lilac up-pointing triangles for simulations without muscles involved; blue squares for passive muscles; as well as green circles, orange diamonds, and red down-pointing triangles for muscle stimulation of u ∈ {0.1, 0.25, 0.5}, respectively. Confidence bands of the regression are shown as pale areas of the corresponding color. The significance of the statistical test is indicated by alongside asterisks (** = significant with 0.001 ≤ p < 0.05, *** = highly significant with p < 0.001).

Figure 5

Compressive (z-)force between each pair of adjacent vertebrae against lumbar lordosis (LL). Colors and marker symbols of the data points and the corresponding regression lines consistently correspond to the modes: lilac up-pointing triangles for simulations without muscles involved; blue squares for passive muscles; as well as green circles, orange diamonds, and red down-pointing triangles for muscle stimulation of u ∈ {0.1, 0.25, 0.5}, respectively. Confidence bands of the regression are shown as pale areas of the corresponding color. The significance of the statistical test is indicated by alongside asterisks (* = tendency with 0.05 ≤ p ≤ 0.1, ** = significant with 0.001 ≤ p < 0.05, *** = highly significant with p < 0.001).

Figure 6

Shear (y-)force between each pair of adjacent vertebrae against lumbar lordosis (LL). Colors and marker symbols of the data points and the corresponding regression lines consistently correspond to the modes: lilac up-pointing triangles for simulations without muscles involved; blue squares for passive muscles; as well as green circles, orange diamonds, and red down-pointing triangles for muscle stimulation of u ∈ {0.1, 0.25, 0.5}, respectively. Confidence bands of the regression are shown as pale areas of the corresponding color.

Figure 7

Bending moments (x-torques) around the transversal axis between each pair of adjacent vertebrae against lumbar lordosis (LL). Colors and marker symbols of the data points and the corresponding regression lines consistently correspond to the modes: lilac up-pointing triangles for simulations without muscles involved; blue squares for passive muscles; as well as green circles, orange diamonds, and red down-pointing triangles for muscle stimulation of u ∈ {0.1, 0.25, 0.5}, respectively. Confidence bands of the regression are shown as pale areas of the corresponding color.

Figure 8

Facet force between each pair of adjacent articular facets against lumbar lordosis (LL). Colors and marker symbols of the data points and the corresponding regression lines consistently correspond to the modes: lilac up-pointing triangles for simulations without muscles involved; blue squares for passive muscles; as well as green circles, orange diamonds, and red down-pointing triangles for muscle stimulation of u ∈ {0.1, 0.25, 0.5}, respectively. The significance of the statistical test is indicated by alongside asterisks (* = tendency with 0.05 ≤ p ≤ 0.1, ** = significant with 0.001 ≤ p < 0.05).