A Robust Numerical Methodology for Fatigue Damage Evolution Simulation in Composites
- PMID: 34204337
- PMCID: PMC8234405
- DOI: 10.3390/ma14123348
A Robust Numerical Methodology for Fatigue Damage Evolution Simulation in Composites
Abstract
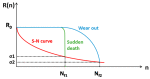
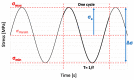
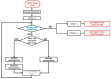
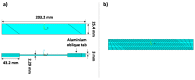
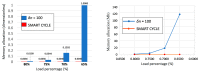
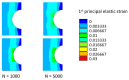
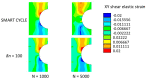
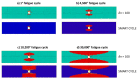
Composite materials, like metals, are subject to fatigue effects, representing one of the main causes for component collapse in carbon fiber-reinforced polymers. Indeed, when subject to low stress cyclic loading, carbon fiber-reinforced polymers exhibit gradual degradation of the mechanical properties. The numerical simulation of this phenomenon, which can strongly reduce time and costs to market, can be extremely expensive in terms of computational effort since a very high number of static analyses need to be run to take into account the real damage propagation due the fatigue effects. In this paper, a novel cycle jump strategy, named Smart Cycle strategy, is introduced in the numerical model to avoid the simulation of every single cycle and save computational resources. This cycle jump strategy can be seen as an enhancement of the empirical model proposed by Shokrieh and Lessard for the evaluation of the fatigue-induced strength and stiffness degradation. Indeed, the Smart Cycle allows quickly obtaining a preliminary assessment of the fatigue behavior of composite structures. It is based on the hypothesis that the stress redistribution, due to the fatigue-induced gradual degradation of the material properties, can be neglected until sudden fiber and/or matrix damage is verified at element/lamina level. The numerical procedure has been implemented in the commercial finite element code ANSYS MECHANICAL, by means of Ansys Parametric Design Languages (APDL). Briefly, the Smart Cycle routine is able to predict cycles where fatigue failure criteria are likely to be satisfied and to limit the numerical simulation to these cycles where a consistent damage propagation in terms of fiber and matrix breakage is expected. The proposed numerical strategy was preliminarily validated, in the frame of this research study, on 30° fiber-oriented unidirectional coupons subjected to tensile-tensile fatigue loading conditions. The numerical results were compared with literature experimental data in terms of number of cycles at failure for different percentage of the static strength. Lastly, in order to assess its potential in terms of computational time saving on more complex structures and different loading conditions, the proposed numerical approach was used to investigate the fatigue behavior of a cross-ply open-hole composite panel under tension-tension fatigue loading conditions.
Keywords: fatigue; open-hole specimen; residual stiffness cycle jump strategy; residual strength.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

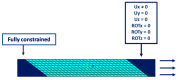



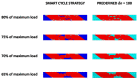
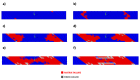
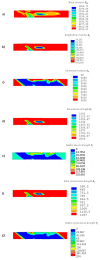







References
-
- Vinson J.R., Chou T.W. Composite Materials and Their Use in Structures. Halsted Press; New York, NY, USA: 1975.
-
- Rana S., Fangueiro R. Advanced Composite Materials for Aerospace Engineering. Woodhead Publishing; Sawstone, UK: 2016. pp. 1–15.
-
- Skoczylas J., Samborski S., Kłonica M. The Application of Composite Materials in the Aerospace Industry. J. Technol. Exploit. Mech. Eng. 2019 doi: 10.35784/jteme.73. - DOI
-
- Pinto F., Meo M. Design and Manufacturing of a Novel Shear Thickening Fluid Composite (STFC) with Enhanced out-of-Plane Properties and Damage Suppression. Appl. Compos. Mater. 2017;24:643–660. doi: 10.1007/s10443-016-9532-1. - DOI
-
- Talreja R., Singh C.V. Damage and Failure of Composite Materials. Cambridge University Press; Cambridge, UK: 2012. pp. 1–304.
Grants and funding
LinkOut - more resources
Full Text Sources

