Cancellation of Auxetic Properties in F.C.C. Hard Sphere Crystals by Hybrid Layer-Channel Nanoinclusions Filled by Hard Spheres of Another Diameter

Abstract

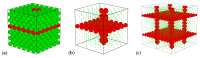
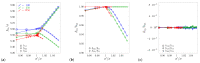
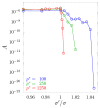
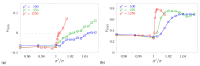
The elastic properties of f.c.c. hard sphere crystals with periodic arrays of nanoinclusions filled by hard spheres of another diameter are the subject of this paper. It has been shown that a simple modification of the model structure is sufficient to cause very significant changes in its elastic properties. The use of inclusions in the form of joined (mutually orthogonal) layers and channels showed that the resulting tetragonal system exhibited a complete lack of auxetic properties when the inclusion spheres reached sufficiently large diameter. Moreover, it was very surprising that this hybrid inclusion, which can completely eliminate auxeticity, was composed of components that, alone, in these conditions, enhanced the auxeticity either slightly (layer) or strongly (channel). The study was performed with computer simulations using the Monte Carlo method in the isothermal-isobaric (NpT) ensemble with a variable box shape.

Keywords: Monte Carlo simulations; auxetics; hard spheres; inclusions; nanochannels; nanolayers; negative Poisson’s ratio.

Figure 1

The unit supercell (f.c.c.) with the matrix and inclusion particles marked, respectively, in green and in red color (a). The inclusion’s structure (b) and the repeated supercell (c). The diameters of the matrix spheres in (b,c) were scaled down to show the underlying structure.

Figure 2

Box matrix elements for all studied values of dimensionless pressure (indicated in different colors). Diagonal components are presented in (a) and their ratios in (b), whereas the off-diagonal components (with relation to $h_{11}$) are presented in (c), which shows that in all cases, one obtains a cuboid box.

Figure 3

The dimensionless elastic compliance matrix elements ($S_{ij}^{*}=k_{\mathrm{B}}T{S}_{ij}/{\sigma }^3$) for different dimensionless pressure values studied in this work: $p^{*}=$ (a) 100, (b) 250, and (c) 1250.

Figure 4

The dimensionless elastic moduli matrix elements ($B_{ij}^{*}=\beta B_{ij}{\sigma }^3$) for different dimensionless pressure values studied in this work: $p^{*}=$ (a) 100, (b) 250, and (c) 1250.

Figure 5

Poisson’s ratio averaged over all $\overrightarrow{\mathbf{m}}$ directions, with external stress applied in selected $\overrightarrow{\mathbf{n}}$ directions: (a) $\left[100\right]$, (b) $\left[110\right]$, and (c) $\left[111\right]$.

Figure 6

The parameter A (see Equation (9)), which may be understood as a volume of a certain space (in the spherical coordinate system) confined by the averaged negative part of the Poisson’s ratio in all possible $\overrightarrow{\mathbf{n}}$-directions.

Figure 7

Global extreme values of Poisson’s ratio for all studied pressures plotted with respect to ${\sigma }^{\prime }/\sigma$. Global extremes are understood as the (a) minimal and (b) maximal Poisson’s ratio found for the system under the given pressure with given ${\sigma }^{\prime }/\sigma$, in any $\overrightarrow{\mathbf{n}}$-direction. The positive sign of ${\nu }_{\min }$ implies that the system is non-auxetic, i.e., there is no direction $\overrightarrow{\mathbf{n}}$ for which the system exhibits an auxetic response in any direction $\overrightarrow{\mathbf{m}}$ transverse to it.

Figure 8

Plots of surfaces of extreme (minimal, bottom row; maximal, top row) and the average (middle row) Poisson’s ratio for given $\overrightarrow{\mathbf{n}}$-direction, as a function of $\theta ,\phi$, for $p^{*}=250$ and selected ${\sigma }^{\prime }/\sigma$ organized in columns from the left (I) $0.95$, (II) 1, (III) $1.025$, (IV) $1.055$. Solid lines on the $\theta -\phi$ plane are isolines for $\nu =0$ (for $\theta ,\phi$ pairs inside these regions, Poisson’s ratio is negative).

Figure 9

Extreme Poisson’s ratio for cubic (upper part) and tetragonal (lower part) systems. Plotted in (a) as two 3D surfaces of the maximal and minimal Poisson’s ratio (similar to (8)). In (b), the surfaces were cut in order to clearly show the internal topology and to mark the location of the typically studied crystallographic directions, as well as the characteristic points on the surfaces, e.g., isotropic Poisson’s ratio points (A) or extreme Poisson’s ratios for a given direction ($B^{\prime }$, $B^{″}$). These values are also marked in (c) as a plot of Poisson’s ratio with respect to the orientation of the $\overrightarrow{\mathbf{m}}$-direction (for the same $\overrightarrow{\mathbf{n}}$-direction as marked in (b)). (d–g) present how the same data can be decomposed and folded in spherical coordinates resulting in the shapes presented in (e–g). The respective points from (b) are also marked here. For clarity, the positive and negative part of the minimal Poisson’s ratio are drawn separately (d,f,g).

Figure 9

Extreme Poisson’s ratio for cubic (upper part) and tetragonal (lower part) systems. Plotted in (a) as two 3D surfaces of the maximal and minimal Poisson’s ratio (similar to (8)). In (b), the surfaces were cut in order to clearly show the internal topology and to mark the location of the typically studied crystallographic directions, as well as the characteristic points on the surfaces, e.g., isotropic Poisson’s ratio points (A) or extreme Poisson’s ratios for a given direction ($B^{\prime }$, $B^{″}$). These values are also marked in (c) as a plot of Poisson’s ratio with respect to the orientation of the $\overrightarrow{\mathbf{m}}$-direction (for the same $\overrightarrow{\mathbf{n}}$-direction as marked in (b)). (d–g) present how the same data can be decomposed and folded in spherical coordinates resulting in the shapes presented in (e–g). The respective points from (b) are also marked here. For clarity, the positive and negative part of the minimal Poisson’s ratio are drawn separately (d,f,g).