Biologically-Based Mathematical Modeling of Tumor Vasculature and Angiogenesis via Time-Resolved Imaging Data
- PMID: 34208448
- PMCID: PMC8234316
- DOI: 10.3390/cancers13123008
Biologically-Based Mathematical Modeling of Tumor Vasculature and Angiogenesis via Time-Resolved Imaging Data
Abstract
Tumor-associated vasculature is responsible for the delivery of nutrients, removal of waste, and allowing growth beyond 2-3 mm3. Additionally, the vascular network, which is changing in both space and time, fundamentally influences tumor response to both systemic and radiation therapy. Thus, a robust understanding of vascular dynamics is necessary to accurately predict tumor growth, as well as establish optimal treatment protocols to achieve optimal tumor control. Such a goal requires the intimate integration of both theory and experiment. Quantitative and time-resolved imaging methods have emerged as technologies able to visualize and characterize tumor vascular properties before and during therapy at the tissue and cell scale. Parallel to, but separate from those developments, mathematical modeling techniques have been developed to enable in silico investigations into theoretical tumor and vascular dynamics. In particular, recent efforts have sought to integrate both theory and experiment to enable data-driven mathematical modeling. Such mathematical models are calibrated by data obtained from individual tumor-vascular systems to predict future vascular growth, delivery of systemic agents, and response to radiotherapy. In this review, we discuss experimental techniques for visualizing and quantifying vascular dynamics including magnetic resonance imaging, microfluidic devices, and confocal microscopy. We then focus on the integration of these experimental measures with biologically based mathematical models to generate testable predictions.
Keywords: computational fluid dynamics; computational oncology; confocal microscopy; magnetic resonance imaging; partial differential equations; perfusion; systems biology; treatment response; vascular growth.
Conflict of interest statement
The authors declare no conflict of interest.
Figures


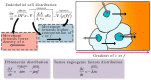
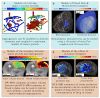
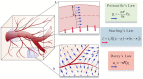
References
-
- Folkman J., Bach M., Rowe J.W., Davidoff F., Lambert P., Hirsch C., Goldberg A., Hiatt H.H., Glass J., Henshaw E. Tumor Angiogenesis—Therapeutic Implications. N. Engl. J. Med. 1971;285:1182–1186. - PubMed
-
- Folkman J. In: Tumor Angiogenesis. Klein G., Weinhouse S., Haddow A.B.T.-A., editors. Volume 19. Academic Press; Cambridge, MA, USA: 1974. pp. 331–358.
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources

