On the Optimal Field Sensing in Near-Field Characterization

Abstract

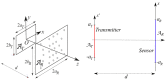
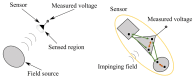
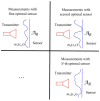
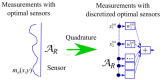
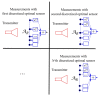
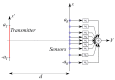
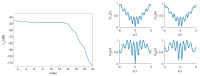
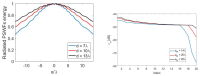
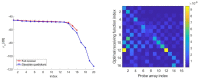
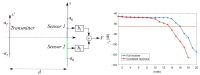
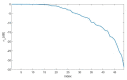
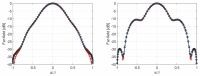
We deal with the problem of characterizing a source or scatterer from electromagnetic radiated or scattered field measurements. The problem refers to the amplitude and phase measurements which has applications also to interferometric approaches at optical frequencies. From low frequencies (microwaves) to high frequencies or optics, application examples are near-field/far-field transformations, object restoration from measurements within a pupil, near-field THz imaging, optical coherence tomography and ptychography. When analyzing the transmitting-sensing system, we can define "optimal virtual" sensors by using the Singular Value Decomposition (SVD) approach which has been, since long time, recognized as the "optimal" tool to manage linear algebraic problems. The problem however emerges of discretizing the relevant singular functions, thus defining the field sampling. To this end, we have recently developed an approach based on the Singular Value Optimization (SVO) technique. To make the "virtual" sensors physically realizable, in this paper, two approaches are considered: casting the "virtual" field sensors into arrays reaching the same performance of the "virtual" ones; operating a segmentation of the receiver. Concerning the array case, two ways are followed: synthesize the array by a generalized Gaussian quadrature discretizing the linear reception functionals and use elementary sensors according to SVO. We show that SVO is "optimal" in the sense that it leads to the use of elementary, non-uniformly located field sensors having the same performance of the "virtual" sensors and that generalized Gaussian quadrature has essentially the same performance.

Keywords: gaussian quadrature; near-field/far-field transformations; optimality; singular value decomposition; singular value optimization; source/scatterer characterization.

Figure 1

Left: geometry of the 3D problem. Right: geometry of the 2D problem.

Figure 2

The sensing process as a scattering one.

Figure 3

Subsequent use of the “optimal virtual” sensors to measure the transmitted field according to Equations (7) and (8).

Figure 4

Illustrating the representation of the “optimal virtual” sensors by arrays thanks to the use of generalized Gaussian quadrature rules.

Figure 5

Subsequent use of the discretized “optimal virtual” sensors to measure the transmitted field.

Figure 6

Illustrating the point-like elements array geometry with weights.

Figure 7

(Left): SVs for the case $a_T=5\lambda$, $a_R=7\lambda$ and $d=7\lambda$. (Right): first four “optimal virtual” sensors for the case $a_T=5\lambda$, $a_R=7\lambda$ and $d=7\lambda$.

Figure 8

(Left): illustrating the spreading of the energy of the PSWFs for the case $a_T=5\lambda$ and $a_R=7\lambda$ and for an increasing distance d. (Right): increasing the size of $a_R$ to catch all the radiated DoFs for the case $a_T=5\lambda$ and $d=10\lambda$.

Figure 9

Optimized Gaussian quadrature points for the case $a_T=5\lambda$, $a_R=7\lambda$, $d=7\lambda$ and $N=20$.

Figure 10

(Left): SVB for the case when “optimal virtual” sensing functions are used, instead of the PSWFs, to form the link matrix and the SVB obtained for the case of point-like elements and use of the “optimal” weights. (Right): percentage errors when the point-like elements when the “optimal” weights are used to form the elements of the link matrix instead of the “optimal virtual” sensors. The rows span the different sets of weights while the columns the possible impinging fields.

Figure 11

SVO points for the case $a_T=5\lambda$, $a_R=7\lambda$, $d=7\lambda$ and $N=20$.

Figure 12

(Left): Illustrating the point-like sensor geometry without weights. (Right): SVO points for the case $a_T=5\lambda$, $a_R=7\lambda$, $d=7\lambda$ and $N=20$.

Figure 13

(Left): Illustrating the “optimal” reception problem for a halved upper aperture. (Right): SVB for the half-sensing aperture case.

Figure 14

(Left): combining the “optimal” half-sensors with weights. (Right): SVB for the two half-sensors apertures combined with weights.

Figure 15

SVs for the horn antenna case.

Figure 16

(Left): Curve of the optimized SVO functional with varying number of sampling points ${\Xi }_{opt}\left(Q\right)$. (Right): SVO sampling points.

Figure 17

Cuts, along the u-axis (left) and v-axis (right), of the reference (red pluses) and reconstructed far-field using “optimal virtual” sensors (black circles) and SVO (blue solid line).