Emergent inequality and business cycles in a simple behavioral macroeconomic model

Abstract

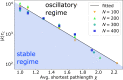
Standard macroeconomic models assume that households are rational in the sense that they are perfect utility maximizers and explain economic dynamics in terms of shocks that drive the economy away from the steady state. Here we build on a standard macroeconomic model in which a single rational representative household makes a savings decision of how much to consume or invest. In our model, households are myopic boundedly rational heterogeneous agents embedded in a social network. From time to time each household updates its savings rate by copying the savings rate of its neighbor with the highest consumption. If the updating time is short, the economy is stuck in a poverty trap, but for longer updating times economic output approaches its optimal value, and we observe a critical transition to an economy with irregular endogenous oscillations in economic output, resembling a business cycle. In this regime households divide into two groups: poor households with low savings rates and rich households with high savings rates. Thus, inequality and economic dynamics both occur spontaneously as a consequence of imperfect household decision-making. Adding a few "rational" agents with a fixed savings rate equal to the long-term optimum allows us to match business cycle timescales. Our work here supports an alternative program of research that substitutes utility maximization for behaviorally grounded decision-making.

Keywords: computational simulation; endogenous business cycles; social learning.

Fig. 1.

The critical transition from the stable regime to the oscillatory regime. We perform an ensemble of simulations at different values of the social interaction time $\tau$, with other parameters held fixed such as $\delta =0.1$ and network topology (see SI Appendix for details). We show a heatmap indicating the probability density of the distribution of individual household’s savings rates for each value of $\tau$, along with the aggregate savings rate $\tilde{s}$. We compare it to the golden rule savings rate $s_{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d}}\hspace{0.17em}=\hspace{0.17em}0.5$ and the savings rate $s^{*}$ predicted by Eq. 4.

Fig. 2.

The endogenous business cycle in the oscillatory regime. We show several time series when $\tau \hspace{0.17em}>\hspace{0.17em}{\tau }_{\mathrm{c}}$. Top Left shows the savings rates $s_i\left(t\right)$ for four randomly chosen households as a function of time, as well as the aggregate savings rate $\tilde{s}$. Middle Left shows the capital $K_i\left(t\right)$ of the same four households as a function of time. Bottom Left shows the cyclic behavior of the aggregate output superimposed on the aggregate savings rate. Top Right, Middle Right, and Bottom Right are histograms of the indicated variables, accumulated over a longer interval.

Fig. 3.

Endogenous dynamics in the oscillatory regime. (A) We plot the average per-capita consumption $c$ against the average per-capita capital $k$ and show the aggregate saving rate $\tilde{s}$ as red when it is greater than 0.5 and blue when it is less than 0.5. The trajectory orbits around the optimal steady state $\left(k^{*},c^{*}\right)$ of the standard RCK model, which is at the intersection of the dashed optimality curve and the solid black $\dot{k}=0$ line. Each dot corresponds to one timestep; the orbit is counterclockwise. (B) An illustration of the cause of the oscillatory dynamics. Top and Bottom show snapshots at two different times as indicated in A. At time $t_1$ the aggregate savings rate is low, aggregate capital is low, and the economy is in a depression; at time $t_2$ the opposite is true. The capital and savings rates of individual households are shown as dots with different colors. There are two clusters, corresponding to rich and poor households. The household that is currently switching its savings rate is indicated by an arrow connecting its previous state to its current state. The dashed black curve indicates the iso-consumption curve for the household $i$ with the highest consumption.

Fig. 4.

The critical social interaction time depends on network properties. The logarithm of the mean number of neighbors $⟨k⟩$ times the critical interaction time ${\tau }_c$ is plotted vs. the average shortest path length $\chi$ for various values of $N$ and $p$, confirming Eq. 6. The stable regime ($\tau \hspace{0.17em}<\hspace{0.17em}{\tau }_c$) is shaded in blue.

Fig. 5.

Business-cycle–like periodicities can emerge from our model. (A and B) We show from Left to Right the histogram of the final savings rates of the households, time series of the effective savings rate $\tilde{s}$ and capital return $r$, and Lomb–Scargle spectrograms averaged over 100 runs. We use a scale-free Barabási–Albert network (44) with $N\hspace{0.17em}=\hspace{0.17em}\mathrm{4,000},\delta =0.2,\tau =1.5,⟨k⟩\hspace{0.17em}=\hspace{0.17em}40$, where $⟨k⟩$ is the mean degree. In A all households change their savings rate, while in B, 5% of households keep it fixed at a long-term optimal rate $s^{*}=2/9$, corresponding to a discount rate $\rho =0.05$.

Fig. 6.

The problem of pole balancing is analogous to the problem of optimizing savings in an otherwise unstable economy. A man attempts to maintain a pole in a vertical position. This is possible if the pole is long enough, but small errors in the control process drive endogenous oscillations in the angle of the pole.