The evolutionary dynamics of viruses: virion release strategies, time delays and fitness minima

Abstract

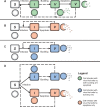
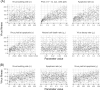
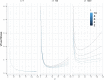
Viruses exhibit a diverse array of strategies for infecting host cells and for virion release after replication. Cell exit strategies generally involve either budding from the cell membrane or killing the host cell. The conditions under which either is at a selective advantage is a key question in the evolutionary theory of viruses, with the outcome having potentially important impacts on the course of infection and pathogenicity. Although a plethora of external factors will influence the fitness of either strategy; here, we focus just on the effects of the physical properties of the system. We develop theoretical approaches to assess the effects of the time delays between initial infection and virion release. We show that the length of the delay before apoptosis is an important trait in virus evolutionary dynamics. Our results show that for a fixed time to apoptosis, intermediate delays lead to virus fitness that is lower than short times to apoptosis - leading to an apoptotic strategy - and long times to apoptosis - leading to a budding strategy at the between-cell level. At fitness minima, selection is expected to be disruptive and the potential for adaptive radiation in virus strategies is feasible. Hence, the physical properties of the system are sufficient to explain the existence of both budding and virus-induced apoptosis. The fitness functions presented here provide a formal basis for further work focusing on the evolutionary implications of trade-offs between time delays, intracellular replication and resulting mutation rates.

Keywords: invasion fitness; mathematical modeling; virus evolution.

Figure 1.

Schematic of models used to obtain virus fitness functions and in evolutionary invasion analysis. (A) The conceptual model for Eq. 1 (no delays) and Eq. 2 (delays). (B) The schematic for the model in Eq. 1 assuming the virus budding rate (λ) is zero and Supplementary Eq. S1 with no virus budding. (C) The schematic for the model in Eq. 1 assuming the apoptosis rate (α) and virus yield at apoptosis (γ) is zero and Supplementary Eq. S2 with no virus-induced apoptosis. (D) The models for budding only and apoptosis only strategies, combined in the evolutionary invasion analysis, where a resident virus that exits cells by budding is invaded by a mutant virus that exits cells by apoptosis (Eqs S15 and S16 of Supplementary Appendix A).

Figure 2.

Virus fitness (Eq. S9, Supplementary Appendix A) for the model without delays (Eq. 1), as a function of each model parameter. Each plot shows virus fitness for 1,000 samples from each parameter range using Latin hypercube sampling and assuming a uniform distribution. Parameter ranges are detailed in Table 1. For the plots in (A) the virus yield at apoptosis (γ) is independent of the apoptosis rate (α), whereas for (B) (γ) scales with $\frac{1}{\alpha }$. See Table 1 for further details of the parameters.

Figure 3.

Evolutionary outcomes for apoptotic versus budding virus as a function of apoptotic virus production rate and: (A) average cell lifespan (μ_C); (B) time to apoptosis ($\frac{1}{\alpha }$ for the model without delays or τ for the model with delays). Results determined by invasion analysis, assuming an apoptotic virus which releases virions by apoptosis invades a virus which releases virions by budding only. Lines represent equivalent fitness—above the line the apoptotic virus can invade, below the line the apoptotic virus cannot invade. The analysis assumed that the virus clearance rate μ_V = 0.1 hours⁻¹, probability of infection $\beta ={10}^{-6}$ and cell death rate μ_C = 1/120 hours⁻¹ (B) or variable (A), were equivalent for both viruses. For both plots, the budding delay τ′ = 1 hour for the resident virus. For (A), the mutant virus apoptosis rate α = 1/24 hours⁻¹ for the model without delays and τ = 24 hours for the model with delays. For (B), the x axis represents the average time to apoptosis (1/α) for the model without delays and τ for the model with delays. The resident virus budding rate (λ) was arbitrarily set to 100 hours⁻¹. We calculated the relative apoptotic intracellular virus production rate by dividing the resulting virus yield at apoptosis (γ) from the invasion analysis by the average or fixed time to apoptosis and then divided this by λ. Equations used to produce this figure are Eqs. S15 and S16 in Supplementary Appendix A.

Figure 4

Virus fitness (Eq. S12, Supplementary Appendix A) for the model without delays (Eq. 2), as a function of each model parameter. Each plot shows virus fitness for 1,000 samples from each parameter range using Latin hypercube sampling and assuming a uniform distribution. Parameter ranges are detailed in Table 1. Samples where the budding delay was greater than the time to apoptosis (τ′ > τ) were omitted.

Figure 5

Virus fitness (Eq. S12, Supplementary Appendix A) for model including delays (Eq. 2) as a function of time to apoptosis (τ). Shorter budding delays (τ′), relative to average cell lifespan (μ_C) and higher budding rates (λ) result in a fitness minimum. Other parameter values kept constant—background cell death rate (μ_C) = 1/24 hours⁻¹, virus clearance rate (μ_V) = 0.1 hours⁻¹, virus yield at apoptosis (γ) = 5,000, probability of susceptible cell infection multiplied by the number of infected cells (βS) = 1.

Figure 6.

Trade-offs in investment in budding yield and yield at apoptosis. (A) Longer times (in hours) to apoptosis (τ) require greater investment in yield (parameters λ  =  0, τ′ = 2). (B) Other things being equal, differences in time delays generate trade-offs in budding yield—yield at apoptosis investment (parameters τ  =  24, τ′ = 2).