Generative hypergraph clustering: From blockmodels to modularity

Abstract

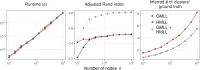
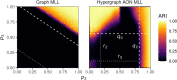
Hypergraphs are a natural modeling paradigm for networked systems with multiway interactions. A standard task in network analysis is the identification of closely related or densely interconnected nodes. We propose a probabilistic generative model of clustered hypergraphs with heterogeneous node degrees and edge sizes. Approximate maximum likelihood inference in this model leads to a clustering objective that generalizes the popular modularity objective for graphs. From this, we derive an inference algorithm that generalizes the Louvain graph community detection method, and a faster, specialized variant in which edges are expected to lie fully within clusters. Using synthetic and empirical data, we demonstrate that the specialized method is highly scalable and can detect clusters where graph-based methods fail. We also use our model to find interpretable higher-order structure in school contact networks, U.S. congressional bill cosponsorship and committees, product categories in copurchasing behavior, and hotel locations from web browsing sessions.

Fig. 1. Runtime, ARI, and number of clusters returned by GMLL and HMLL in a synthetic testbed with optimal affinity parameters.

The within-cluster edge placement probabilities are p₂ = 3/5, p₃ = 1/n³, and p₄ = 1/n⁴. We also show in light gray the results obtained by using GMLL as a preprocessing step, whose output partition is then refined by HMLL (light gray).

Fig. 2. Detectability experiments in synthetic hypergraphs.

For i = 2,3, p_i is the proportion of within-cluster edges of size i. Each pixel gives the mean ARI over 20 independently generated DCHSBMs of size n = 500 where each node is incident to, on average, five 2-edges and five 3-edges. (Left) The recovered partition $\widehat{\mathbf{z}}$ is obtained from GMLL. (Right) The recovered partition is obtained from AON HMLL (algorithm S1). The dashed and dotted lines give various detectability thresholds as described in the main text. In each panel, the returned partition $\widehat{\mathbf{z}}$ is the highest-likelihood partition from 20 alternations between updating $\widehat{\mathbf{z}}$ and inference of the affinity parameters. In this experiment only, we incorporate a regularization term $-n\text{log}\overline{\mathrm{\ell }}$ in the modularity objective to promote label vectors z with fewer clusters.

Fig. 3. Comparison of clustering algorithms in contact-primary-school and contact-high-school.

For each dataset, we show a partition obtained from the classical graph Louvain modularity maximization heuristic, a partition obtained from GMLL, and partition obtained by AON HMLL. The partition shown is the one that attains the corresponding objective function after 20 rounds of iterative likelihood maximization. Each box records the number of agents with the specified combination of inferred cluster and ground truth label. The bottom row visualizes the number m_k of edges of size k, the inferred size weights β_k, and inferred resolution parameters γ_k as defined in (15). On the far right, γ_k0 = m_k/vol(H)^k.

Fig. 4. Comparison of hypergraph AON MLL (algorithm S1) against dyadic likelihood Louvain in data with known clusters.

Points give the ARI of the highest-likelihood partition obtained after 20 alternations between partitioning and parameter estimation. The maximum edge size $\overline{\mathit{k}}$ varies along the horizontal axis. In the panel titles, n is the number of nodes and m the number of edges when $\overline{\mathit{k}}=25$. Note that the vertical axis limits vary between panels.