Sequence-specific minimizers via polar sets

Abstract

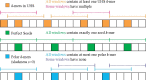
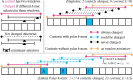
Motivation: Minimizers are efficient methods to sample k-mers from genomic sequences that unconditionally preserve sufficiently long matches between sequences. Well-established methods to construct efficient minimizers focus on sampling fewer k-mers on a random sequence and use universal hitting sets (sets of k-mers that appear frequently enough) to upper bound the sketch size. In contrast, the problem of sequence-specific minimizers, which is to construct efficient minimizers to sample fewer k-mers on a specific sequence such as the reference genome, is less studied. Currently, the theoretical understanding of this problem is lacking, and existing methods do not specialize well to sketch specific sequences.

Results: We propose the concept of polar sets, complementary to the existing idea of universal hitting sets. Polar sets are k-mer sets that are spread out enough on the reference, and provably specialize well to specific sequences. Link energy measures how well spread out a polar set is, and with it, the sketch size can be bounded from above and below in a theoretically sound way. This allows for direct optimization of sketch size. We propose efficient heuristics to construct polar sets, and via experiments on the human reference genome, show their practical superiority in designing efficient sequence-specific minimizers.

Availability and implementation: A reference implementation and code for analyses under an open-source license are at https://github.com/kingsford-group/polarset.

Supplementary information: Supplementary data are available at Bioinformatics online.

Fig. 1.

Comparing universal hitting sets, perfect seeds (compatible minimizers become perfect minimizers) and polar sets. Each block indicates a k-mer, and each segment indicates a window of length 5 (w = 5). To provide a better contrast with universal hitting sets, we show polar sets with slackness s = 0 (see Definition 2)

Fig. 2.

Examples for our argument for the polar set density bound with w = 5. Left top: Legend for a context, and when it is charged. Right top: Case for a singleton polar k-mer without links. In this case, $L(S,A)=0$. Bottom: Case for three linked polar k-mers. Whatever the ordering between the three polar k-mers, two of the four contexts marked in blue will be charged. The link energy $L(S,A)=1/3$: A and B are l = 3 bases away with energy $2l/(w+1)-1=0$, B and C are l = 4 bases away with energy $2l/(w+1)-1=1/3$

Fig. 3.

Examples of layered polar sets, with three layers. Without layered polar sets, the k-mers from layer 2 and 3 could not be selected as in the polar set because of self-collision. The whole sequence is covered in this case (every window contains a polar k-mer from one layer). Layer 1 is the one with highest priority and our layered heuristics construct it first

Fig. 4.

(A) Energy surplus and deficit for short (w = 10) and for long (w = 100) windows, computed on the human reference sequence hg38. The difference between the two lines is the difference between the upper and lower bound of Theorem 1. It is very small and the bounds are very good estimates in practice. (B) Density factor for the proposed methods, for short and long windows, computed on hg38. The bottom orange dashed line is the theoretical minimum density (perfect minimizers)