Characterization of real-world networks through quantum potentials
- PMID: 34255791
- PMCID: PMC8277057
- DOI: 10.1371/journal.pone.0254384
Characterization of real-world networks through quantum potentials
Abstract
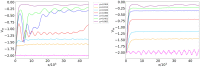
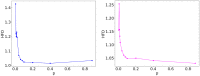
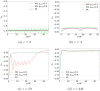
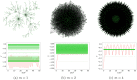
Network connectivity has been thoroughly investigated in several domains, including physics, neuroscience, and social sciences. This work tackles the possibility of characterizing the topological properties of real-world networks from a quantum-inspired perspective. Starting from the normalized Laplacian of a network, we use a well-defined procedure, based on the dressing transformations, to derive a 1-dimensional Schrödinger-like equation characterized by the same eigenvalues. We investigate the shape and properties of the potential appearing in this equation in simulated small-world and scale-free network ensembles, using measures of fractality. Besides, we employ the proposed framework to compare real-world networks with the Erdős-Rényi, Watts-Strogatz and Barabási-Albert benchmark models. Reconstructed potentials allow to assess to which extent real-world networks approach these models, providing further insight on their formation mechanisms and connectivity properties.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


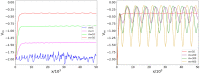


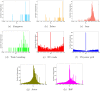
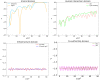
References
-
- Newman ME. The structure and function of complex networks. SIAM review. 2003;45(2):167–256. doi: 10.1137/S003614450342480 - DOI
-
- Barabási AL, Pósfai M. Network science. Cambridge University Press; 2016. Available from: http://barabasi.com/networksciencebook/.
-
- Albert R, Barabási AL. Statistical mechanics of complex networks. Reviews of Modern Physics. 2002;74(1):47. doi: 10.1103/RevModPhys.74.47 - DOI
MeSH terms
LinkOut - more resources
Full Text Sources

