Reinforcement learning control of a biomechanical model of the upper extremity

Abstract

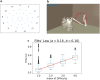
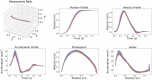
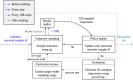
Among the infinite number of possible movements that can be produced, humans are commonly assumed to choose those that optimize criteria such as minimizing movement time, subject to certain movement constraints like signal-dependent and constant motor noise. While so far these assumptions have only been evaluated for simplified point-mass or planar models, we address the question of whether they can predict reaching movements in a full skeletal model of the human upper extremity. We learn a control policy using a motor babbling approach as implemented in reinforcement learning, using aimed movements of the tip of the right index finger towards randomly placed 3D targets of varying size. We use a state-of-the-art biomechanical model, which includes seven actuated degrees of freedom. To deal with the curse of dimensionality, we use a simplified second-order muscle model, acting at each degree of freedom instead of individual muscles. The results confirm that the assumptions of signal-dependent and constant motor noise, together with the objective of movement time minimization, are sufficient for a state-of-the-art skeletal model of the human upper extremity to reproduce complex phenomena of human movement, in particular Fitts' Law and the [Formula: see text] Power Law. This result supports the notion that control of the complex human biomechanical system can plausibly be determined by a set of simple assumptions and can easily be learned.

Figure 1

Synthesized reaching movement. A policy implemented as a neural network computes motor control signals of simplified muscles at the joints of a biomechanical upper extremity model from observations of the current state of the upper body. We use Deep Reinforcement Learning to learn a policy that reaches random targets in minimal time, given signal-dependent and constant motor noise.

Figure 2

Fitts’ Law type task. (a) The target setup in the discrete Fitts’ Law type task follows the ISO 9241-9 ergonomics standard. Different circles correspond to different IDs and distances between targets. (b) Visualization of our biomechanical model performing aimed movements. Note that for each time step, only the current target (position and radius) is given to the learned policy. (c) The movements generated by our learned policy conform to Fitts’ Law. Here, movement time is plotted against ID for all distances and IDs in the considered ISO task (6500 movements in total).

Figure 3

Elliptic via-point task. Elliptic movements generated by our learned policy conform to the $\frac{2}{3}$ Power Law. (a) End-effector positions projected onto the 2D space (blue dots), where targets were subsequently placed along an ellipse of 15 cm width and 6 cm height (red curve). (b) Log-log regression of velocity against radius of curvature for end-effector positions sampled with 100 Hz when tracing the ellipse for 60 s.

Figure 4

End-effector trajectories (ID 4). 3D path, projected position, velocity, acceleration, phasespace, and Hooke plots of 50 aimed movements (between targets 7 and 8 shown in Fig. 2a) with ID 4 and a target distance of 35 cm.

Figure 5

End-effector trajectories (ID 2). 3D path, projected position, velocity, acceleration, phasespace, and Hooke plots of 50 aimed movements (between targets 7 and 8 shown in Fig. 2a) with ID 2 and a target distance of 35 cm.

Figure 6

Neuronal network architectures. (a) The actor network takes a state s as input and returns the policy ${\pi }_{\theta }$ in terms of mean and standard deviation of the seven normal distributions, from which the components of the action vector are drawn. (b) The critic network takes both state s and action vector a as input and returns the estimated state-action value. Two critic networks are trained simultaneously to improve the speed and stability of learning (Double Q-Learning). Detailed information about the input state components are given in the Methods section.

Figure 7

Reinforcement learning procedure. Before training, the networks are initialized with random weights $\theta$, and 10 K transitions are generated using the resulting initial policy. These are stored in the replay buffer (blue dashed arrows). During training (red dotted box), trajectory sampling and policy update steps are executed alternately in each step. The targets used in the trajectory sampling part are generated by the curriculum learner, which is updated every 10K steps, based on an evaluation of the most recent (greedy) policy. As soon as the target width suggested by the curriculum learner falls below 1 cm, the training phase is completed and the final policy ${\pi }_{{\theta }^{\ast }}$ is returned (teal dash-dotted arrow).