Reaction Path-Force Matching in Collective Variables: Determining Ab Initio QM/MM Free Energy Profiles by Fitting Mean Force

Abstract

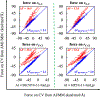
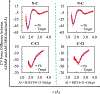
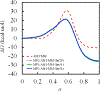
First-principles determination of free energy profiles for condensed-phase chemical reactions is hampered by the daunting costs associated with configurational sampling on ab initio quantum mechanical/molecular mechanical (AI/MM) potential energy surfaces. Here, we report a new method that enables efficient AI/MM free energy simulations through mean force fitting. In this method, a free energy path in collective variables (CVs) is first determined on an efficient reactive aiding potential. Based on the configurations sampled along the free energy path, correcting forces to reproduce the AI/MM forces on the CVs are determined through force matching. The AI/MM free energy profile is then predicted from simulations on the aiding potential in conjunction with the correcting forces. Such cycles of correction-prediction are repeated until convergence is established. As the instantaneous forces on the CVs sampled in equilibrium ensembles along the free energy path are fitted, this procedure faithfully restores the target free energy profile by reproducing the free energy mean forces. Due to its close connection with the reaction path-force matching (RP-FM) framework recently introduced by us, we designate the new method as RP-FM in collective variables (RP-FM-CV). We demonstrate the effectiveness of this method on a type-II solution-phase SN₂ reaction, NH₃ + CH₃Cl (the Menshutkin reaction), simulated with an explicit water solvent. To obtain the AI/MM free energy profiles, we employed the semiempirical AM1/MM Hamiltonian as the base level for determining the string minimum free energy pathway, along which the free energy mean forces are fitted to various target AI/MM levels using the Hartree-Fock (HF) theory, density functional theory (DFT), and the second-order Møller-Plesset perturbation (MP2) theory as the AI method. The forces on the bond-breaking and bond-forming CVs at both the base and target levels are obtained by force transformation from Cartesian to redundant internal coordinates under the Wilson B-matrix formalism, where the linearized FM is facilitated by the use of spline functions. For the Menshutkin reaction tested, our FM treatment greatly reduces the deviations on the CV forces, originally in the range of 12-33 to ∼2 kcal/mol/Å. Comparisons with the experimental and benchmark AI/MM results, tests of the new method under a variety of simulation protocols, and analyses of the solute-solvent radial distribution functions suggest that RP-FM-CV can be used as an efficient, accurate, and robust method for simulating solution-phase chemical reactions.

Figure 1.

Schematic representation of the RP-FM-CV method.

Figure 2.

Menshutkin reaction between ammonia and methyl chloride (NH₃ + CH₃Cl → CH₃NH₃⁺ + Cl^-).

Figure 3.

Free energy profiles along the string MFEPs (with α=0 being the reactant and 1 being the product) from the AM1/MM (dashed red) and RP-FM-CV simulations of the Menshutkin reaction in aqueous solution. Results from the RP-FM-CV AI:AM1/MM simulations were obtained by matching AM1/MM forces on the CVs to various target AI/MM levels using the default 6–31+G(d,p) basis set: B3LYP:AM1/MM (dotted black), BH&HLYP:AM1/MM (green with circles), and MP2:AM1/MM (solid blue).

Figure 4.

Internal force correlations between the base AM1/MM and target AI/MM methods [at the B3LYP/MM and MP2/MM levels both using the 6–31+G(d,p) basis set]: before (red squares) and after (blue circles) applying the RP-FM-CV internal force corrections; the corresponding trend lines are shown as dashed and solid lines. Internal forces on the two bond CVs were computed based on 300 configurations sampled along the condensed-phase MFEP from the AM1/MM string simulations. The average internal force deviations (ΔF; in kcal/mol/Å) between the base and target levels, before (red) and after (blue) force matching, are also shown for comparison.

Figure 5.

Internal force corrections on CVs for the Menshutkin reaction in solution with AM1/MM being the base level and the target forces obtained at the B3LYP/MM and MP2/MM levels using the 6–31+G(d,p) basis set. Both the actual internal force differences (based on 300 solution-phase configurations along the string MFEP) between the base and target levels (labeled “Target”; red triangles) and the spline-based force corrections (labeled “Fit”; blue lines) resulting from FM are shown for each CV (i.e., the N-C and C-Cl bonds).

Figure 6.

Various redundant internal coordinate schemes tested for the RP-FM-CV simulations of the Menshutkin reaction in solution. The two distance-based CVs for bond forming and breaking, i.e., N-C (1–5) and C-Cl (5–9) (shown in red in the “Bonds” section), are used consistently in both the string MFEP simulations and the FM calculations.

Figure 7.

Free energy profiles for the Menshutkin reaction in solution obtained from the RP-FM-CV simulations at the MP2:AM1/MM level by using different redundant internal coordinate sets; the AM1/MM profile (dashed red) is shown for comparison. The RP-FM-CV results obtained using 28 (Int28; dotted black), 31 (Int31; solid green with circles), and 34 (Int34; solid blue) internal coordinates are shown (see Figure 6 for the definitions of the three schemes).

Figure 8.

Free energy profiles for the Menshutkin reaction in solution obtained from the RP-FM-CV simulations at the MP2:AM1/MM level using different sample sizes for FM; the AM1/MM profile (dashed red) is shown for comparison. The RP-FM-CV results with FM in CVs conducted using 300 (FM-300; dotted black), 1500 (FM-1500; green with circles), 3000 (FM-3000; solid blue), and 15000 (FM15000; pink with crosses) configurations are shown.

Figure 9.

Free energy profiles for the Menshutkin reaction in solution obtained from the RP-FM-CV simulations by matching the AM1/MM forces on CVs to those determined at the MP2/MM level using various basis sets, including 6–31G(d), 6–31+G(d,p), 6–311++G(d,p), and 6–311++G(2df,2p).

Figure 10.

Minimum free energy paths (MFEPs) for the Menshutkin reaction in solution for the free energy profiles shown in Figure 3. The MFEPs from the RP-FM-CV AI:AM1/MM simulations were obtained by matching the AM1/MM forces on the CVs to various target AI/MM levels using the 6–31+G(d,p) basis set: B3LYP:AM1/MM (dotted black), BH&HLYP:AM1/MM (green with circles), and MP2:AM1/MM (solid blue), compared with AM1/MM (dashed red). The transition states (TSs) located on the MFEPs are also marked: B3LYP:AM1/MM (square), BH&HLYP:AM1/MM (triangle), MP2:AM1/MM (diamond), and AM1/MM (circle).

Figure 11.

Free energy profiles for the Menshutkin reaction in solution obtained from the RP-FM-CV simulations at the MP2:AM1/MM level using the 6–31+G(d,p) basis set over five consecutive RP and FM cycles: the first (dotted black), second (green with circles), third (solid blue), fourth (pink with crosses), and fifth (light blue with triangles) cycles, compared with AM1/MM (dashed red).

Figure 12.

Solute-solvent radial distribution functions (RDFs) obtained from the RP-FM-CV simulations at the MP2:AM1/MM level using the 6–31+G(d,p) basis set, compared with the AM1/MM results. The RDFs for the solute (heavy atoms) and solvent (water oxygens: O_w) (i.e., N-O_w, C-O_w, and Cl-O_w) determined using an average of 3,600 configurations in each regions are shown: reactant (R; dotted red), transition state (TS; solid green), and product (P; dashed blue).