Magnetic-resonance-based measurement of electromagnetic fields and conductivity in vivo using single current administration-A machine learning approach
- PMID: 34293014
- PMCID: PMC8297925
- DOI: 10.1371/journal.pone.0254690
Magnetic-resonance-based measurement of electromagnetic fields and conductivity in vivo using single current administration-A machine learning approach
Abstract
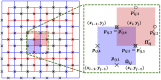
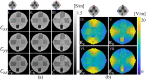
Diffusion tensor magnetic resonance electrical impedance tomography (DT-MREIT) is a newly developed technique that combines MR-based measurements of magnetic flux density with diffusion tensor MRI (DT-MRI) data to reconstruct electrical conductivity tensor distributions. DT-MREIT techniques normally require injection of two independent current patterns for unique reconstruction of conductivity characteristics. In this paper, we demonstrate an algorithm that can be used to reconstruct the position dependent scale factor relating conductivity and diffusion tensors, using flux density data measured from only one current injection. We demonstrate how these images can also be used to reconstruct electric field and current density distributions. Reconstructions were performed using a mimetic algorithm and simulations of magnetic flux density from complementary electrode montages, combined with a small-scale machine learning approach. In a biological tissue phantom, we found that the method reduced relative errors between single-current and two-current DT-MREIT results to around 10%. For in vivo human experimental data the error was about 15%. These results suggest that incorporation of machine learning may make it easier to recover electrical conductivity tensors and electric field images during neuromodulation therapy without the need for multiple current administrations.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures







Similar articles
-
Software Toolbox for Low-Frequency Conductivity and Current Density Imaging Using MRI.IEEE Trans Biomed Eng. 2017 Nov;64(11):2505-2514. doi: 10.1109/TBME.2017.2732502. IEEE Trans Biomed Eng. 2017. PMID: 28767360
-
Low-frequency conductivity tensor imaging with a single current injection using DT-MREIT.Phys Med Biol. 2021 Feb 20;66(5):055011. doi: 10.1088/1361-6560/abddcf. Phys Med Biol. 2021. PMID: 33472190
-
Anisotropic Conductivity Tensor Imaging of In Vivo Canine Brain Using DT-MREIT.IEEE Trans Med Imaging. 2017 Jan;36(1):124-131. doi: 10.1109/TMI.2016.2598546. IEEE Trans Med Imaging. 2017. PMID: 28055828
-
Magnetic resonance electrical impedance tomography (MREIT) for high-resolution conductivity imaging.Physiol Meas. 2008 Oct;29(10):R1-26. doi: 10.1088/0967-3334/29/10/R01. Epub 2008 Sep 17. Physiol Meas. 2008. PMID: 18799834 Review.
-
A review of anisotropic conductivity models of brain white matter based on diffusion tensor imaging.Med Biol Eng Comput. 2018 Aug;56(8):1325-1332. doi: 10.1007/s11517-018-1845-9. Epub 2018 Jun 1. Med Biol Eng Comput. 2018. PMID: 29855784 Review.
Cited by
-
Mini Review: Impedance Measurement in Neuroscience and Its Prospective Application in the Field of Surgical Neurooncology.Front Neurol. 2022 Jan 17;12:825012. doi: 10.3389/fneur.2021.825012. eCollection 2021. Front Neurol. 2022. PMID: 35111132 Free PMC article. Review.
-
Use of machine learning to improve the estimation of conductivity and permittivity based on longitudinal relaxation time T1 in magnetic resonance at 7 T.Sci Rep. 2023 May 15;13(1):7837. doi: 10.1038/s41598-023-35104-9. Sci Rep. 2023. PMID: 37188769 Free PMC article.
-
Magnetic Resonance Electrical Impedance Tomography.Adv Exp Med Biol. 2022;1380:157-183. doi: 10.1007/978-3-031-03873-0_7. Adv Exp Med Biol. 2022. PMID: 36306098
-
Enhanced magnetic transduction of neuronal activity by nanofabricated inductors quantified via finite element analysis.J Neural Eng. 2022 Jul 1;19(4):10.1088/1741-2552/ac7907. doi: 10.1088/1741-2552/ac7907. J Neural Eng. 2022. PMID: 35705065 Free PMC article.
-
Validation of conductivity tensor imaging against diffusion tensor magnetic resonance electrical impedance tomography.Sci Rep. 2024 Aug 3;14(1):17995. doi: 10.1038/s41598-024-68551-z. Sci Rep. 2024. PMID: 39097661 Free PMC article.
References
-
- Seo JK, Woo EJ. Magnetic resonance electrical impedance tomography. SIAM Rev. 2011; 53(1):40–68. doi: 10.1137/080742932 - DOI
-
- Joy MLG, Scott GC and Henkelman M. In vivo detection of applied electric currents by magnetic resonnace imaging. Magn. Reson. Imaging. 1989; 7(1):89–94. - PubMed
-
- Scott GC et al.. Sensitivity of magnetic resonance current density imaging. J. Magn. Reson. 1992; 97(2):235–254. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

