Spin defects in hBN as promising temperature, pressure and magnetic field quantum sensors

Abstract

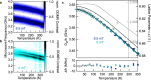
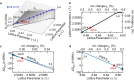
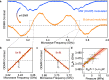
Spin defects in solid-state materials are strong candidate systems for quantum information technology and sensing applications. Here we explore in details the recently discovered negatively charged boron vacancies (V_B^-) in hexagonal boron nitride (hBN) and demonstrate their use as atomic scale sensors for temperature, magnetic fields and externally applied pressure. These applications are possible due to the high-spin triplet ground state and bright spin-dependent photoluminescence of the V_B^-. Specifically, we find that the frequency shift in optically detected magnetic resonance measurements is not only sensitive to static magnetic fields, but also to temperature and pressure changes which we relate to crystal lattice parameters. We show that spin-rich hBN films are potentially applicable as intrinsic sensors in heterostructures made of functionalized 2D materials.

Fig. 1. Schematic of the hexagonal boron nitride (hBN).

a Alternating boron (red) and nitrogen (blue) atoms and the lattice constants a and c. b Lattice contraction and expansion due to temperature variation, according to crystallographic data. c cw ODMR spectra measured with (dark blue) and without (cyan) external magnetic field at different temperatures T = 295, 160, and 10 K. Lowering of the temperature causes the resonances ${\nu }_0,{\nu }_1$ and ${\nu }_2$ to shift to larger microwave frequencies indicating an increase of the zero-field splitting $D_{gs}$.

Fig. 2. Temperature dependence of the ODMR spectrum of V⁻_B.

Color maps represent the peak positions of the normalized ODMR spectrum for different temperatures in an external magnetic field of a B = 8.5 mT and b B = 0 mT. c ZFS parameter $D_{gs}/h$ obtained from a (blue diamonds) and b (cyan diamonds) vs. temperature. The monotonic increase while lowering the sample temperature is unaffected by the magnetic field. The data can be fitted using Eq. (2) describing the temperature-dependent change of the lattice parameters a (gray dotted line) and c (black dotted line) that are also plotted in (c). The fits are shown as solid lines (blue for 8.5 mT and cyan for 0 mT) on top of the diamonds and reproduce the temperature dependence perfectly. (bottom panel) The difference between measurements and fit (Δ/h).

Fig. 3. Zero-field splitting dependence on the lattice parameters a and c.

a Combined three-dimensional representation of plots (b−d) with the slopes ${\theta }_a$and ${\theta }_c$ (shown also (c, d)). Equation (2) is fitted (solid lines) to the experimental data displayed as diamonds. The ZFS reference temperature T = 295 K is marked by the red dot. The assignment of colors of fitting lines (blue for 8.5 mT and cyan for 0 mT) is the same as in Fig. 2. b Comparison of lattice parameters in the temperature range 5−350 K. c Change of ZFS $△D_{gs,a}$ caused by the temperature-dependent lattice parameter $a$. d Change of ZFS $△D_{gs,c}$ caused by temperature-dependent lattice parameter c.

Fig. 4. Pressure dependence of the zero-field splitting parameter D_gs/h.

a ODMR spectra of ${\mathrm{V}}_{\mathrm{B}}^{-}$ with microwave modulation (on/off) (blue) and sinusoidal magnetic field modulation (orange). The partially resolved hyperfine peaks are blurred due to an intentional overmodulation of the spectrum (for details see Supplementary Fig. 4) that allows a linear fit in the vicinity of the zero-crossings for a precise determination of the resonant transitions ${\mathrm{\nu }}_1$ (b) and ${\mathrm{\nu }}_2$ (c) and therefore the parameter $D_{gs}/h$. d $D_{gs}/h$ as a function of pressure, follows a slope of (1.16 ± 0.15) $\mathrm{Hz}/\mathrm{Pa}$ which is close to the expected value (0.91 ± 0.20) $\mathrm{Hz}/\mathrm{Pa}$ according to Eq. (15). Vertical error bars represent the standard deviations of the linear fits for ${\mathrm{\nu }}_1$and ${\mathrm{\nu }}_2$ in panels (b, c). Horizontal error bars indicate the uncertainty of the determination of the sample area to which the pressure is applied.

Fig. 5. Experimental (diamonds) and simulated (dark and light blue traces) resonant frequencies of V⁻_B for different temperatures and magnetic fields.

a ODMR measurements (pink diamonds) at B < 20 mT. b cw EPR measurement at T = 5 K and microwave frequency of 9.4 GHz (light green) and electron spin-echo measurements at T = 8 K and 94 GHz (dark green). Note the axes are shifted for better visibility and comparability.