Errors in Statistical Inference Under Model Misspecification: Evidence, Hypothesis Testing, and AIC
- PMID: 34295904
- PMCID: PMC8293863
- DOI: 10.3389/fevo.2019.00372
Errors in Statistical Inference Under Model Misspecification: Evidence, Hypothesis Testing, and AIC
Abstract
The methods for making statistical inferences in scientific analysis have diversified even within the frequentist branch of statistics, but comparison has been elusive. We approximate analytically and numerically the performance of Neyman-Pearson hypothesis testing, Fisher significance testing, information criteria, and evidential statistics (Royall, 1997). This last approach is implemented in the form of evidence functions: statistics for comparing two models by estimating, based on data, their relative distance to the generating process (i.e., truth) (Lele, 2004). A consequence of this definition is the salient property that the probabilities of misleading or weak evidence, error probabilities analogous to Type 1 and Type 2 errors in hypothesis testing, all approach 0 as sample size increases. Our comparison of these approaches focuses primarily on the frequency with which errors are made, both when models are correctly specified, and when they are misspecified, but also considers ease of interpretation. The error rates in evidential analysis all decrease to 0 as sample size increases even under model misspecification. Neyman-Pearson testing on the other hand, exhibits great difficulties under misspecification. The real Type 1 and Type 2 error rates can be less, equal to, or greater than the nominal rates depending on the nature of model misspecification. Under some reasonable circumstances, the probability of Type 1 error is an increasing function of sample size that can even approach 1! In contrast, under model misspecification an evidential analysis retains the desirable properties of always having a greater probability of selecting the best model over an inferior one and of having the probability of selecting the best model increase monotonically with sample size. We show that the evidence function concept fulfills the seeming objectives of model selection in ecology, both in a statistical as well as scientific sense, and that evidence functions are intuitive and easily grasped. We find that consistent information criteria are evidence functions but the MSE minimizing (or efficient) information criteria (e.g., AIC, AICc, TIC) are not. The error properties of the MSE minimizing criteria switch between those of evidence functions and those of Neyman-Pearson tests depending on models being compared.
Keywords: Akaike’s information criterion; Kullback-Leibler divergence; error rates in model selection; evidence; evidential statistics; hypothesis testing; model misspecification; model selection.
Conflict of interest statement
Conflict of Interest: The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures

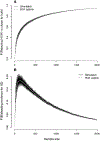


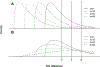

References
-
- Akaike H (1973). “Information theory as an extension of the maximum likelihood principle,” in Second International Symposium on Information Theory, eds Petrov B, and Csaki F (Budapest: Akademiai Kiado; ), 267–281.
-
- Akaike H (1974). A new look at statistical-model identification. IEEE Trans. Autom. Control 19, 716–723. doi: 10.1109/TAC.1974.1100705 - DOI
-
- Akaike H (1981). Likelihood of a model and information criteria. J. Econ 16, 3–14. doi: 10.1016/0304-4076(81)90071-3 - DOI
-
- Anderson D, Burnham K, and Thompson W (2000). Null hypothesis testing: problems, prevalence, and an alternative. J. Wildl. Manag 64, 912–923. doi: 10.2307/3803199 - DOI
Grants and funding
LinkOut - more resources
Full Text Sources
