Anomalous Lehmann Rotation of Achiral Nematic Liquid Crystal Droplets Trapped under Linearly Polarized Optical Tweezers

Abstract

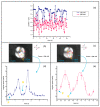
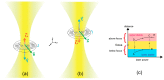
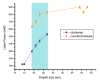
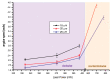
Continuous rotation of a cholesteric droplet under the heat gradient was observed by Lehmann in 1900. This phenomenon, the so-called Lehmann effect, consists of unidirectional rotation around the heat flux axis. We investigate this gradient heat effect using infrared laser optical tweezers. By applying single trap linearly polarized optical tweezers onto a radial achiral nematic liquid crystal droplet, trapping of the droplet was performed. However, under a linearly polarized optical trap, instead of stable trapping of the droplet with slightly deformed molecular directors along with a radial hedgehog defect, anomalous continuous rotation of the droplet was observed. Under low power laser trapping, the droplet appeared to rotate clockwise. By continuously increasing the laser power, a stable trap was observed, followed by reverse directional rotation in a higher intensity laser trap. Optical levitation of the droplet in the laser beam caused the heat gradient, and a breaking of the symmetry of the achiral nematic droplet. These two effects together led to the rotation of the droplet under linearly polarized laser trapping, with the sense of rotation depending on laser power.

Keywords: Lehmann effect; Lehmann rotation; achiral nematic; liquid crystals; optical tweezers.

Figure 1

Schematic illustration of the optical tweezers setup on an inverted microscope.

Figure 2

Microscopic images taken under crossed polarizers and a one-wavelength plate inserted diagonally for director orientation mapping. (a) A 19-μm radial NLC droplet suspended in water. The droplet configuration is spherically symmetric, the so-called ‘radial hedgehog’. (b) By applying the linearly polarized laser onto the droplet, the defect in the middle shifted slightly to the side along the polarization direction of the laser, β = 135° with respect to a horizontal direction. This distorted configuration caused by the alignment of the molecules in the laser beam pointed toward the laser polarization direction, thus pushing the defect to the side.

Figure 3

An NLC droplet under linearly polarized laser trap was found rotating clockwise at laser power 298 mW. The laser polarization direction was set at an angle β = 135° with respect to the horizontal (Supplementary video available).

Figure 4

(a) Plot of the radial hedgehog defect position of 19-μm NLC droplet. The position r was measured with respect to the center of the elliptical trajectory (shown in (b,c)), during clockwise rotation at 298 mW and 338 mW. The period of rotation was 4.54 s and 1.79 s for 298 mW and 338 mW, respectively. (b,c) Tracking of the elliptical trajectory of the defect showing non-uniform angular speed. (d,e) Angular speed of the defect at 298 mW and 338 mW, respectively. The defect rotation was very slow at points P and Q along the direction of laser polarization for 298 mW laser trapping. The effect is less severe for higher laser power.

Figure 5

The same 19-μm NLC droplet as in Figure 3 rotated in the reverse direction under the same linearly polarized laser trap at a higher laser power of 635 mW (Supplementary video available).

Figure 6

Schematic illustration of the droplet position at (a) low power and (b) higher power of a laser when slowly increasing the power of the trapping laser. $\stackrel{\rightharpoonup }{\mathrm{G}}$ represents direction of temperature gradient due to laser intensity. The temperature gradient points toward the laser focus. $\stackrel{\rightharpoonup }{\mathrm{n}}$ is the direction of average molecular directors of the distorted radial droplet. $\stackrel{\rightharpoonup }{\tau }$ is torque direction of the droplet from $\stackrel{\rightharpoonup }{\tau }=\nu \stackrel{\rightharpoonup }{\mathrm{n}}\times \left(\stackrel{\rightharpoonup }{\mathrm{n}}\times \stackrel{\rightharpoonup }{\mathrm{G}}\right)$, which resulted in clockwise rotation in (a) and counterclockwise rotation in (b). (c) Particle position with laser power illustrated roughly the observation of Ashkin’s experiment in optical levitation [15].

Figure 7

Plot of threshold laser power for droplet rotation in clockwise and counterclockwise directions with droplet size. Notice that there is no counterclockwise rotation of small droplets at high power since the droplets were too small, so they were pushed off the trap at high power. There is no clockwise rotation of larger droplets at low power because the droplets were too heavy for rotation. The force from a low power laser could be too small to initiate droplet motion.

Figure 8

Plot of angular speed with laser power of a radial hedgehog defect under linearly polarized laser tweezers. Notice that we can only record one set of data for counterclockwise rotation for each droplet size since the power range for counterclockwise rotation is very small and by increasing the laser power higher than the last data plotted, the droplet was pushed out of the laser trap. For an 18 μm droplet, no counterclockwise rotation was observed, analogous to the observation in Figure 7.