On the Influence of Viscoelastic Modeling in Fluid Flow Simulations of Gum Acrylonitrile Butadiene Rubber

Abstract

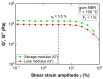
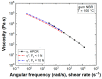
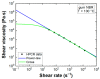
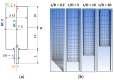
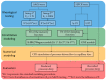
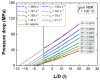
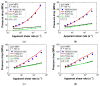
Computational fluid dynamics (CFD) simulation is an important tool as it enables engineers to study different design options without a time-consuming experimental workload. However, the prediction accuracy of any CFD simulation depends upon the set boundary conditions and upon the applied rheological constitutive equation. In the present study the viscoelastic nature of an unfilled gum acrylonitrile butadiene rubber (NBR) is considered by applying the integral and time-dependent Kaye-Bernstein-Kearsley-Zapas (K-BKZ) rheological model. First, exhaustive testing is carried out in the linear viscoelastic (LVE) and non-LVE deformation range including small amplitude oscillatory shear (SAOS) as well as high pressure capillary rheometer (HPCR) tests. Next, three abrupt capillary dies and one tapered orifice die are modeled in Ansys POLYFLOW. The pressure prediction accuracy of the K-BKZ/Wagner model was found to be excellent and insensitive to the applied normal force in SAOS testing as well as to the relation of first and second normal stress differences, provided that damping parameters are fitted to steady-state rheological data. Moreover, the crucial importance of viscoelastic modeling is proven for rubber materials, as two generalized Newtonian fluid (GNF) flow models severely underestimate measured pressure data, especially in contraction flow-dominated geometries.

Keywords: K-BKZ model; computational rheology; rubber rheology; viscoelastic modeling.

Figure A1

(a) Image of gum NBR (PERBUNAN^® 3965 F) delivered as bale; (b) scanning electron microscope (SEM) image of an exemplary compression molded sample ($\varnothing$ = 8 mm, thickness = 1 mm) of gum NBR.

Figure A2

Exemplary amplitude sweep measurement performed with the MCR 501 device at 100 °C to detect the linear viscoelastic deformation range of gum NBR, with the selected shear strain rate of 3.5% for the frequency sweep measurements.

Figure A3

(a) Time-temperature superposition of the phase angle $\delta$ and corresponding Arrhenius plot; (b) K-BKZ model predictions of storage ${\mathrm{G}}^{\prime }$ and loss ${\mathrm{G}}^{″}$ moduli compared to experimental data at the reference temperature T_ref; K-BKZ fit 2 represents fitted LVE data measured at F_n = 10 N.

Figure A4

Complex viscosities ${\mathsf{\eta }}^{*}$ compared to steady-state shear viscosity η.

Figure A5

Light microscope images of strands extruded through an abrupt capillary die with a length-to-diameter (L/D) ratio of 10/1 at an apparent shear rate level of (a) 27 s⁻¹; (b) 30906 s⁻¹.

Figure A6

Recorded pressure in the L/D = 10/1 capillary die in dependence of the measurement time with apparent shear rate levels displayed ranging from 27 s⁻¹ to 3906 s⁻¹.

Figure A7

Steady-state shear viscosity of gum NBR compared to power-law and Cross model predictions.

Figure 1

(a) Computational fluid dynamic (CFD) simulation setup including boundary conditions (BCs) 1 to 4, dimensions, and position of the pressure transducer (p); (b) Meshes for the tapered orifice (L/D = 0.2/1; ϕ = 90°) and three abrupt capillary dies (L/D = 5/1, 10/1, 20/1; ϕ = 180°) utilized in numerical calculations.

Figure 2

Flow chart displaying the research design of the present study.

Figure 3

(a) Effect of applied normal force (F_n) on the sample during the measurement and influence of the measurement devices (RPA vs. MCR 501) on the complex viscosity of gum NBR; (b) No influence of sample preparation detected on the complex viscosity of gum NBR.

Figure 4

(a) Time-temperature superposition of the dissipation factor ($\tan \mathsf{\delta }$) and corresponding Arrhenius plot; (b) K-BKZ model predictions of storage G’ and loss G” moduli compared to experimental data at the reference temperature T_ref; K-BKZ fit 1 represents LVE data measured at a normal force (F_n) < 1 N.

Figure 5

Entrance pressure corrected flow curves of two capillary dies with same length-to-diameter (L/D) ratios but different capillary diameters.

Figure 6

Measured pressure drops for various apparent shear rates (${\dot{\mathsf{\gamma }}}_{\mathrm{a}}$) in dependence of the capillary die length (Bagley plot) including linear approximations (Lin. approx.) with coefficients of determination (R²).

Figure 7

Steady-state shear (η) and uniaxial elongational (${\mathsf{\eta }}_{\mathrm{e}}$) viscosities of gum NBR compared to K-BKZ model predictions; K-BKZ fit 1 represents fitted LVE data measured at F_n < 1 N ($\mathsf{\theta }$ = 0), K-BKZ fit 2 represents fitted LVE data measured at F_n = 10 N ($\mathsf{\theta }$ = 0), and K-BKZ fit 3 represents fitted LVE data measured at F_n < 1 N ($\mathsf{\theta }$ = −0.15).

Figure 8

Measured pressure data compared to CFD simulation results; K-BKZ fit 1 represents fitted LVE data measured at F_n < 1 N ($\mathsf{\theta }$ = 0), K-BKZ fit 2 represents fitted LVE data measured at F_n = 10 N ($\mathsf{\theta }$ = 0), and K-BKZ fit 3 represents fitted LVE data measured at F_n < 1 N ($\mathsf{\theta }$ = −0.15).

Figure 9

Measured pressure data compared to CFD simulation results of the (a) tapered orifice die (L/D = 0.2/1); (b) abrupt capillary die with a length-to-diameter (L/D) ratio of 5/1; (c) abrupt capillary die with L/D = 10/1; (d) abrupt capillary die with L/D = 20/1.