A mechanistic and data-driven reconstruction of the time-varying reproduction number: Application to the COVID-19 epidemic
- PMID: 34310593
- PMCID: PMC8341713
- DOI: 10.1371/journal.pcbi.1009211
A mechanistic and data-driven reconstruction of the time-varying reproduction number: Application to the COVID-19 epidemic
Abstract
The effective reproduction number Reff is a critical epidemiological parameter that characterizes the transmissibility of a pathogen. However, this parameter is difficult to estimate in the presence of silent transmission and/or significant temporal variation in case reporting. This variation can occur due to the lack of timely or appropriate testing, public health interventions and/or changes in human behavior during an epidemic. This is exactly the situation we are confronted with during this COVID-19 pandemic. In this work, we propose to estimate Reff for the SARS-CoV-2 (the etiological agent of the COVID-19), based on a model of its propagation considering a time-varying transmission rate. This rate is modeled by a Brownian diffusion process embedded in a stochastic model. The model is then fitted by Bayesian inference (particle Markov Chain Monte Carlo method) using multiple well-documented hospital datasets from several regions in France and in Ireland. This mechanistic modeling framework enables us to reconstruct the temporal evolution of the transmission rate of the COVID-19 based only on the available data. Except for the specific model structure, it is non-specifically assumed that the transmission rate follows a basic stochastic process constrained by the observations. This approach allows us to follow both the course of the COVID-19 epidemic and the temporal evolution of its Reff(t). Besides, it allows to assess and to interpret the evolution of transmission with respect to the mitigation strategies implemented to control the epidemic waves in France and in Ireland. We can thus estimate a reduction of more than 80% for the first wave in all the studied regions but a smaller reduction for the second wave when the epidemic was less active, around 45% in France but just 20% in Ireland. For the third wave in Ireland the reduction was again significant (>70%).
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
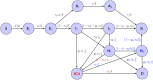


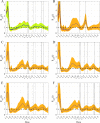
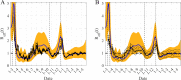
References
-
- Heesterbeek JAP, Dietz K. The concept of R0 in epidemic theory. Statistica Neerlandica. 1996:50;89–110. doi: 10.1111/j.1467-9574.1996.tb01482.x - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
Miscellaneous

