Explaining distortions in metacognition with an attractor network model of decision uncertainty

Abstract

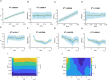
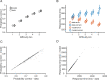
Metacognition is the ability to reflect on, and evaluate, our cognition and behaviour. Distortions in metacognition are common in mental health disorders, though the neural underpinnings of such dysfunction are unknown. One reason for this is that models of key components of metacognition, such as decision confidence, are generally specified at an algorithmic or process level. While such models can be used to relate brain function to psychopathology, they are difficult to map to a neurobiological mechanism. Here, we develop a biologically-plausible model of decision uncertainty in an attempt to bridge this gap. We first relate the model's uncertainty in perceptual decisions to standard metrics of metacognition, namely mean confidence level (bias) and the accuracy of metacognitive judgments (sensitivity). We show that dissociable shifts in metacognition are associated with isolated disturbances at higher-order levels of a circuit associated with self-monitoring, akin to neuropsychological findings that highlight the detrimental effect of prefrontal brain lesions on metacognitive performance. Notably, we are able to account for empirical confidence judgements by fitting the parameters of our biophysical model to first-order performance data, specifically choice and response times. Lastly, in a reanalysis of existing data we show that self-reported mental health symptoms relate to disturbances in an uncertainty-monitoring component of the network. By bridging a gap between a biologically-plausible model of confidence formation and observed disturbances of metacognition in mental health disorders we provide a first step towards mapping theoretical constructs of metacognition onto dynamical models of decision uncertainty. In doing so, we provide a computational framework for modelling metacognitive performance in settings where access to explicit confidence reports is not possible.

Fig 1. Task and neural circuit model.

A. Perceptual decision-making task used as a basis for simulations. A fixation cross appears for 1000ms, followed by two boxes with dots for a fixed duration of 300ms. Subjects are asked to judge which box contains the greater number of dots by pressing left/right key on the keyboard. Their response is highlighted for 500ms, i.e. with a blue border appearing around the chosen box. Finally, participants report their confidence in their decision on a scale of 1–11 in experiment 1, and 1–6 in experiment 2 (S1 and S2 Appendices). B. Neural circuit model of decision uncertainty. The model comprises two modules. The sensorimotor module (green) comprises two neuronal populations (blue/orange) selective for right/left information. The two populations are endowed with mutual inhibition (lines with filled circles) and self-excitation (curved arrows). These populations receive external input as a function of the difference between the number of dots shown in the two boxes. Figure assumes correct response is on the right–hence the positive input bias for the population selective to rightward information. A gain parameter controls the difference in input each population receives. One neuronal population (red) continuously monitors overall decision uncertainty by integrating the summed output of the sensorimotor populations (see Methods). Uncertainty is equally fed back into both neuronal populations through symmetric feedback excitation (two-way red arrows, controlled by value of uncertainty modulation strength, UM). C. A sample timecourse of the activities of the sensorimotor populations (top panel) and uncertainty-monitoring population (bottom panel). Typical winner-take-all behaviour is seen in the sensorimotor module. Activity of the uncertainty-monitoring population follows a phasic profile (see [39,40] and Methods). Trial simulated with dot difference between the two boxes set at 20 (see Methods). D. Sample timecourse of firing rates of the ‘winning’ neural population (i.e. one with more input bias) in the sensorimotor module under two strengths of uncertainty-modulation (UM) values. Random seed reset to control for noise. In the case of the trial with strong (weak) excitatory feedback (solid grey (black) trace), ramping up is faster (slower), leading to a quicker (slower) response. Neural population firing rates shown here are smoothed with a simple moving average (window size = 50ms).

Fig 2. Dissociable changes in metacognition are associated with changes in uncertainty modulation.

The behaviour of the model was analysed using standard metrics of performance (d’) and metacognition (metacognitive bias, sensitivity (meta_d’) and efficiency (meta_d’/d’)). Blue line represents mean value of metric across 50 simulations. Shaded area is standard deviation. Yellow line is linear fit to mean value of metric as a function of parameter value. Increases in gain lead to monotonic increases in (A) d′(β₁ = 0.5, R² = 0.99, p<0.001) and (C) metacognitive sensitivity (β₁ = 28.45, R² = 0.99, p<0.001) but (B) a small effect on bias (β₁ = 23.5, R² = 0.09, p<0.001). Gain has a moderate positive weak negative effect on (D) metacognitive efficiency (β₁ = 3.53, R² = 0.41, p<0.001), possibly driven by the strong linear increase in d’ in panel A. Increasing UM has no effect on (E) d′(β₁ = 5.65, R² = 0.01, p = 0.15), but a negative effect on (F) metacognitive bias (β₁ = −122.83, R² = 0.2, p<0.001), (G) metacognitive sensitivity (β₁ = −98.83, R² = 0.5, p<0.001), and (H) metacognitive efficiency (β₁ = −100.49, R² = 0.58, p<0.001). In (I-J), we varied both parameters and measured the effect on (I) d′ and (J) metacognitive sensitivity. The increase in d′ is mostly driven by changes in gain (I), whereas changes in metacognitive sensitivity are mostly driven by UM (J). All simulations were done with the same fixed list of dot differences (2.8 in log-space). In simulations (A-H), where the gain (UM) parameter is varied, UM (gain) was fixed at 0.0009 (0.0029). R² in all panels is adjusted R². Confidence data was generated by binning the uncertainty values into 6 bins, assuming equal bin width (see Methods). See Fig D in S5 Appendix for additional simulations with different parameter values. See also S5 Appendix for results that highlight dissociable changes in metacognitive bias as a result of varying UM.

Fig 3. Model accounts for subjects’ perceptual performance in experiment 1.

A. Choice accuracy, i.e. probability correct as a function of task difficulty from experiment 1 of [32] averaged across all 498 participants. Task difficulty is split into 5 difficulty bins (1: most difficult, 5: easiest) as in the original paper (see Methods). Grey markers: data. Black markers: model fits. B. Response times as a function of task difficulty from the data (circles) and model fits (diamonds) averaged across all participants. Orange (blue) markers: Error (correct) responses. The typical ‘<‘ pattern, i.e. response times for correct (error) responses increasing (decreasing) as a function of task difficulty, is found in both the model and data. C. Scatter plot of observed (empirical) vs. simulated overall accuracy and D. response times for each of the 498 subjects. Error bars indicate 95% confidence interval. Random seed is reset after each simulation during the fitting procedure and for the purposes of generating panels C and D (but not A and B). See Fig C in S5 Appendix for scatter plots without resetting the random generator seed.

Fig 4. Model accounts for subjects’ confidence reports and individual differences in uncertainty modulation predict symptom scores.

A. Confidence reports averaged across all participants from experiment 1 data (circles) and model (diamond) as a function of task difficulty. Orange (blue) markers: Error (correct) responses. Note that the model was fit only to first-order performance data (accuracy and response times) and fits to confidence represent an out-of-sample prediction. Confidence increases (decreases) as a function of changing task difficulty for correct (error) responses. B. Symptom scores from experiment 1 were entered into a multiple regression model predicting the strength of uncertainty modulation and gain parameters from the model fits to task performance (choices and response times). Self-report measures of depression (grey), schizotopy (blue), social anxiety (red), obsessive and compulsive symptoms (purple) and generalised anxiety (green) are significantly associated with weaker uncertainty modulation. No significant association was found between impulsivity (pink) and the strength of uncertainty modulation. No significant association was found between the symptom scores and the gain parameter. See Methods for details on the regression models. Error bars indicate s.e.m. All regression results shown control for the influence of age, gender, and IQ (see Fig B in S5 Appendix for regression model results with age and IQ predicting model parameters). * p<0.05.

Fig 5. UM parameter offers an implicit, low-dimensional marker of metacognitive (dys)function.

Symptom scores from experiment 1 were entered into a multiple regression model predicting the strength of uncertainty modulation, empirical mean confidence, and metacognitive sensitivity. Self-report measures of depression (grey), schizotopy (blue), social anxiety (red), obsessive and compulsive symptoms (purple) and generalised anxiety (green) are significantly associated with weaker uncertainty modulation. Depression, social anxiety, and generalised anxiety are associated with lower mean confidence. Depression and generalised anxiety are associated with decreased metacognitive sensitivity. * p<0.05.