Optimal design of cluster randomized trials allowing unequal allocation of clusters and unequal cluster size between arms

Abstract

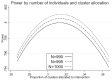
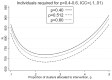
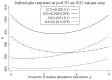
There are sometimes cost, scientific, or logistical reasons to allocate individuals unequally in an individually randomized trial. In cluster randomized trials we can allocate clusters unequally and/or allow different cluster size between trial arms. We consider parallel group designs with a continuous outcome, and optimal designs that require the smallest number of individuals to be measured given the number of clusters. Previous authors have derived the optimal allocation ratio for clusters under different variance and/or intracluster correlations (ICCs) between arms, allowing different but prespecified cluster sizes by arm. We derive closed-form expressions to identify the optimal proportions of clusters and of individuals measured for each arm, thereby defining optimal cluster sizes, when cluster size can be chosen freely. When ICCs differ between arms but the variance is equal, the optimal design allocates more than half the clusters to the arm with the higher ICC, but (typically only slightly) less than half the individuals and hence a smaller cluster size. We also describe optimal design under constraints on the number of clusters or cluster size in one or both arms. This methodology allows trialists to consider a range for the number of clusters in the trial and for each to identify the optimal design. Except if there is clear prior evidence for the ICC and variance by arm, a range of values will need to be considered. Researchers should choose a design with adequate power across the range, while also keeping enough clusters in each arm to permit the intended analysis method.

Keywords: cluster randomized trial; optimal design; power; sample size; unequal allocation.

Figure 1

Power for a total of K = 30 clusters as g and N vary, for a fixed cluster size in one arm (m₁ = 45), effect size d = 0.278, 5% significance level, and ICCs ρ₀ = 0.1, ρ₁ = 0.01

Figure 2

Number of individuals measured, N, as p and g vary from optimal: K = 40 clusters, 80% power, 5% significance level, effect size d = 0.278, and ICCs ρ₀ = 0.1, ρ₁ = 0.01

Figure 3

Number of individuals measured, N, for different ICC values and varying g: K = 40 clusters, 80% power, effect size d = 0.278, and p = 0.51