Novel mechanism for oscillations in catchbonded motor-filament complexes

Abstract

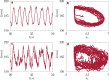
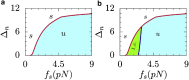
Generation of mechanical oscillations is ubiquitous to a wide variety of intracellular processes, ranging from activity of muscle fibers to oscillations of the mitotic spindle. The activity of motors plays a vital role in maintaining the integrity of the mitotic spindle structure and generating spontaneous oscillations. Although the structural features and properties of the individual motors are well characterized, their implications on the functional behavior of motor-filament complexes are more involved. We show that force-induced allosteric deformations in dynein, which result in catchbonding behavior, provide a generic mechanism to generate spontaneous oscillations in motor-cytoskeletal filament complexes. The resultant phase diagram of such motor-filament systems-characterized by force-induced allosteric deformations-exhibits bistability and sustained limit-cycle oscillations in biologically relevant regimes, such as for catchbonded dynein. The results reported here elucidate the central role of this mechanism in fashioning a distinctive stability behavior and oscillations in motor-filament complexes such as mitotic spindles.

Figure 1

Schematic diagram of the antiparallel MT-motor complex in presence of passive cross-linkers (P). Unbound motors (U) attach to any of the MTs with rate $k_b^{3D}$; bound motors (B) cross-link at rate k_b, whereas they detach from the MT at a rate $k_u^0$. Cross-linked motors (C) become bound motors with detachment rate k_u under a load force F_p. To see this figure in color, go online.

Figure 2

Limit-cycle oscillations for (a) n_c (red curve) and n_b (blue curve) and (b) l as a function of time. The figures show that these quantities oscillate between n_c ∼3–6, n_b ∼20–26, and l ∼164–205 nm. (c) and (d) depict the variation of l and n_b with n_c, respectively (red curves). The blue and green dashed lines depict two sample trajectories with different initial conditions eventually falling onto the limit cycle. All the curves are obtained for f_s = 2.46, Δ_n = 6, which corresponds to a point denoted by a solid diamond in the limit-cycle region in Fig. 3d. To see this figure in color, go online.

Figure 3

Stability diagram of an MT-motor complex as a function of $\widetilde{f_0}$. (a) $\widetilde{f_0}$ = 309.52 (f₀ ≈ 1000 pN), (b) $\widetilde{f_0}$ = 24.76 (f₀ ≈ 80 pN), (c) $\widetilde{f_0}$ = 15.47 (f₀ ≈ pN), and (d) $\widetilde{f_0}$ = 11.98 (f₀ ≈ 38.7 pN). All other parameters are N_p = 100, k_b = $k_u^0$ = 1/s (֒γ = 1), v₀ = 100 nm/s, $\widetilde{\text{Γ}}$ = 2.6, $\widetilde{f_d}$ = 0.2 (f_d ≈ 0.67 pN), α = 68, $\widetilde{f_m}$ = 0.43 (f_m ≈ 1.4 pN), b = 1.3 nm, ε = 2k_BT. The red solid line depicts the boundary between linearly stable (white) and unstable (cyan) regions. Green areas indicate regions where limit cycles can be sustained, and yellow shaded areas signal regions where the complex displays bistable behavior. (e)–(h) depict the unbinding rate of a single dynein motor under load force, f, for the f₀-values of (a)–(d), and the blue dashed line gives the reference curve when f_s = f_m. (i)–(l) show the bifurcations diagrams as a function of f_s in different regions of the phase plane, as indicated by the dashed lines in (a)–(c). The solid blue lines indicate a stable branch, and the dashed red lines indicate unstable solutions. To see this figure in color, go online.

Figure 4

Limit-cycle oscillations in l-time plane (left panels) and in l-n_c plane (right panels) in presence of noise (Eqs. 12, 13, and 14). The values of the diffusion coefficient are λ = 0.1 (in a and b) and λ = 1 (in c and d). All other parameter values are same as Fig. 2. To see this figure in color, go online.

Figure 5

(a) and (b) show the amplitude of oscillations of n_c and l, respectively, and (c) depicts the time period of limit-cycle oscillations as a function of f_s for Δ_n = 1.5. The green dashed line denotes the limit-cycle boundary for the particular set of parameters. All other parameters are same as Fig. 3d. To see this figure in color, go online.

Figure 6

Stability diagram when f_s = f_m (a) in the absence of catchbond ($\widetilde{f_0}$ = 309.52) and (b) presence of catchbond ($\widetilde{f_0}$ = 11.98). All other parameters are same as Fig. 3. The red solid curve corresponds to the boundary between linearly stable (white) and linearly unstable regions (cyan). The figure shows that limit cycles (green) develop only because of catchbond. To see this figure in color, go online.