Modelling the ability of mass drug administration to interrupt soil-transmitted helminth transmission: Community-based deworming in Kenya as a case study

Abstract

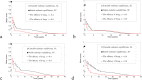
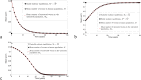
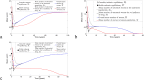
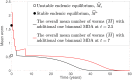
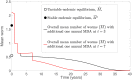
The World Health Organization has recommended the application of mass drug administration (MDA) in treating high prevalence neglected tropical diseases such as soil-transmitted helminths (STHs), schistosomiasis, lymphatic filariasis, onchocerciasis and trachoma. MDA-which is safe, effective and inexpensive-has been widely applied to eliminate or interrupt the transmission of STHs in particular and has been offered to people in endemic regions without requiring individual diagnosis. We propose two mathematical models to investigate the impact of MDA on the mean number of worms in both treated and untreated human subpopulations. By varying the efficay of drugs, initial conditions of the models, coverage and frequency of MDA (both annual and biannual), we examine the dynamic behaviour of both models and the possibility of interruption of transmission. Both models predict that the interruption of transmission is possible if the drug efficacy is sufficiently high, but STH infection remains endemic if the drug efficacy is sufficiently low. In between these two critical values, the two models produce different predictions. By applying an additional round of biannual and annual MDA, we find that interruption of transmission is likely to happen in both cases with lower drug efficacy. In order to interrupt the transmission of STH or eliminate the infection efficiently and effectively, it is crucial to identify the appropriate efficacy of drug, coverage, frequency, timing and number of rounds of MDA.

Fig 1. Numerical solutions of the endemic equilibria M_eq as a function of R₀ with different k values, fixing z = 0.96.

Fig 2. Transmission dynamics of model (3) and (4) considering no application of MDA and one round of MDA at time t = 1 with k = 0.05 and R₀ = 2.

(a) M₀ < M_*. (b) M_* < M₀ < M*. (c) M₀ = M*. (d) M₀ > M*.

Fig 3. Transmission dynamics of model (3) and (4) by considering the implementation of biannual and annual MDA, M₀ > M_*, varying ϵ and choosing z = 0.96, R₀ = 2 and ω = 0.5.

Top row: biannual MDA. Bottom row: annual MDA. Left column: k = 0.05. Right column: k = 0.5.

Fig 4. The comparison of the overestimate (5) and (6) and original model (3) and (4) by considering the implementation of biannual MDA with ϵ = 0.4 and ω = 0.5 and varying k and R₀ values.

(a) R₀ = 2, k = 0.05, n > 5.83 and MSE = 0.1258 × 10⁻⁴. (b) R₀ = 2, k = 0.5, n > 8.34 and MSE = 0.2167 × 10⁻². (c) R₀ = 1.8, k = 0.05, n > 2.86 and MSE = 0.5217 × 10⁻⁶. (d) R₀ = 1.8, k = 0.5, n > 5.38 and MSE = 0.6392 × 10⁻³.

Fig 5. The comparison of solutions (5) and (6) and numerical solutions of model (3) and (4) by considering the implementation of annual MDA with ϵ = 0.4 and ω = 0.5 and varying k and R₀ values.

(a) R₀ = 2, k = 0.05, n > 7.29 and MSE = 0.6333 × 10⁻⁴. (b) R₀ = 2, k = 0.5, n > 13.14 and MSE = 0.0156. (c) R₀ = 1.8, k = 0.05, n > 2.96 and MSE = 0.2106 × 10⁻⁵. (d) R₀ = 1.8, k = 0.5, n > 6.29 and MSE = 0.2264 × 10⁻².

Fig 6. The comparison of models (3) and (9) when no control strategy has been applied.

Both models have the same outcomes for arbitrary initial points, R₀ = 2 and k = 0.05. (a) M₀ > M* and $M_{nt0}>{\widehat{M}}_{*}$. (b) M_* < M₀ < M* and ${\widehat{M}}_{*}<M_{nt0}<{\widehat{M}}^{*}$. (c) M₀ < M_* and $M_{nt0}<{\widehat{M}}_{*}$.

Fig 7. The transmission dynamics of model (9) and (10) for a range of M^0>M^*, ϵ and ω values, with k = 0.05 and R₀ = 2.

(a) ω = ϵ = 0.6 and ${\widehat{M}}_{*}<{\widehat{M}}_0<{\widehat{M}}^{*}$. (b) ω = ϵ = 0.6 and ${\widehat{M}}_0>{\widehat{M}}^{*}$. (c) ${\widehat{M}}_0$ around the neighbourhood of ${\widehat{M}}_{*}$.

Fig 8. Numerical comparison of model (12) and (13) and model (9) and (10) by considering the implementation of biannual MDA with ϵ = ω = 0.6 and varying k and R₀ values.

(a) k = 0.05, R₀ = 1.8 and MSE for M_nt and M_t are 5.9377 × 10⁻⁵ and 1.1881 × 10⁻⁵, respectively. (b) k = 0.2, R₀ = 1.8 and MSE for M_nt and M_t are 1.5909 × 10⁻³ and 2.2534 × 10⁻⁴, respectively. (c) k = 0.05, R₀ = 2 and MSE for M_nt and M_t are 2.6274 × 10⁻⁴ and 2.9925 × 10⁻⁵, respectively. (d) k = 0.2, R₀ = 2 and MSE for M_nt and M_t are 4.5018 × 10⁻³ and 4.7219 × 10⁻⁴, respectively.

Fig 9. Numerical comparison of model (12) and (13) and model (9) and (10) for annual MDA with ϵ = ω = 0.6 and varying k and R₀ values.

(a) k = 0.05, R₀ = 1.8 and MSE for M_nt and M_t are 1.4241 × 10⁻⁴ and 4.9371 × 10⁻⁵, respectively. (b) k = 0.2, R₀ = 1.8 and MSE for M_nt and M_t are 3.2954 × 10⁻³ and 9.5671 × 10⁻⁴, respectively. (c) k = 0.05, R₀ = 2 and MSE for M_nt and M_t are 4.3739 × 10⁻⁴ and 1.1943 × 10⁻⁴, respectively. (d) k = 0.2, R₀ = 2 and MSE for M_nt and M_t are 8.6585 × 10⁻³ and 2.1309 × 10⁻³, respectively.

Fig 10. Numerical results of model (3) and (4) and model (9) and (10) by varying ϵ and applying the coverage of MDA data from the TUMIKIA community-based biannual deworming control strategy.

(a) Disease persistence if ϵ < 0.44. (b) Disease extinction is possible if ϵ ≥ 0.61. (c) Disease extinction is possible for model (3) and (4) if ϵ ≥ 0.44, but the disease will remain in endemic state for model (9) and (10) if ϵ < 0.61.

Fig 11. The numerical results of model (3) and (4) and model (9) and (10) by varying ϵ and applying the coverage of MDA data from the TUMIKIA community-based annual deworming control strategy.

(a) Disease persistence if ϵ < 0.73. (b) Disease extinction if ϵ ≥ 0.85. (c) Disease elimination is possible for model (3) and (4) if ϵ ≥ 0.73, but the disease will remain in endemic state for model (9) and (10) if ϵ < 0.85.

Fig 12. Numerical solutions of model (9) and (10) with an additional round of TUMIKIA community-based biannual deworming strategy.

Fig 13. Numerical solutions of model (9) and (10) with an additional round of TUMIKIA community-based annual deworming strategy.