Finding successful strategies in a complex urban sustainability game

Abstract

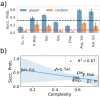
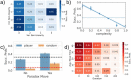
The adverse effects of unsustainable behaviors on human society are leading to an increasingly urgent and critical need to change policies and practices worldwide. This requires that citizens become informed and engaged in participatory governance and measures leading to sustainable futures. Citizens' understanding of the inherent complexity of sustainable systems is a necessary (though generally not sufficient) ingredient for them to understand controversial public policies and maintain the core principles of democratic societies. In this work, we present a novel, open-ended experiment where individuals had the opportunity to solve model urban sustainability problems in a purposeful game. Participants were challenged to interact with familiar LEGO blocks representing elements in a complex generative urban economic indicators model. Players seeks to find a specific urban configuration satisfying particular sustainability requirements. We show that, despite the intrinsic complexity and non-linearity of the problems, participants' ability to make counter-intuitive actions helps them find suitable solutions. Moreover, we show that through successive iterations of the experiment, participants can overcome the difficulties linked to non-linearity and increase the probability of finding the correct solution to the problem. We contend that this kind of what-if platforms could have a crucial role in future approaches to sustainable developments goals.

Figure 1

(a) Example of the interface. The mathematical model’s input is based on the number of bricks for each colour present in the building area. This input is displayed in the horizontal bars on the left part. The more the bricks of a specific colour, the more the bar would be filled. The outputs used to generate missions are shown in the right part of the interface. A green placeholder indicated their current value. Whenever one of the indicators became the target of a mission, a red placeholder appeared to guide the player towards the objective. (b) The installation with two gaming stations. Each gaming station had five containers to store bricks (i), a building area (ii) with an RGB/depth-sensor (iii) above it, a feedback monitor (iv) with a red button to control it (v). Brick containers (i) had labels attached on top providing a brief explanation of the brick colour meaning (e.g., “Orange bricks represents the population of the city”). (c) Scheme of user interaction during a mission. Once the player has modified the city and pressed the button, the RGB/dept-sensor translates the bricks’ number into the generative model’s input. The output is then computed as the most likely value of the probability distribution of the outputs conditioned on the input. The input corresponding to the different brick colours and the outputs are then updated simultaneously on the feedback monitor.

Figure 2

(a) Probability of success for the different mission types. Mission types are sorted in descending order according to their average complexity. Blue bars represent the results obtained with real players data, while orange bars represent those of the random agent. The black horizontal dashed line is the overall probability of success for real players, while the red one is for the random agent. Error bars have been computed as the standard error for a probability f, defined as $\sqrt{f(1-f)/n}$ where n is the size of the sample. (b) Correlation between the chances of accomplishing a specific mission type and its average Complexity. The solid line represents a linear regression between the two variables with the corresponding $R^2$ reported in the legend. The shaded area represents the 5–95% confidence interval. The mission labels in both panels correspond to the missions: Increase Quality of Life (QoL); Increase Employment Rate (Emp.); Increase Percentage of Highly-Educated individuals (%H. Ed.); Increase the Average Salary (Avg. Sal.); Decrease Economic Inequality (Ec. In.); Decrease the Number of Private Cars (P. Mob.); Decrease the produced Garbage (Gar.).

Figure 3

(a) Success probability as a function of Initial Non-Linearity and Variation of Non-Linearity. Success probability of a match vs. match complexity (b) and the presence of a paradox move (c). In (c), blue bars represent the results obtained with real players data, while orange bars result from the random agent. The horizontal dashed line (blue in (b) and black in (c)) is the overall probability of success for real players. The red horizontal dashed line in (c) is the probability of success for the random agent. Error bars have been computed as the standard error for a probability f, defined as $\sqrt{f(1-f)/n}$ where n is the size of the sample. The Paradox Move feature is defined using the experts’ survey results. (d) Success probability as a function of Duration and Average Move Time. Both these quantities are measured in seconds.

Figure 4

(Top) Increase of the success probability as a function of the match number. (Bottom) Odds ratios of the different features for predicting a successful match, for all matches together (first column) and each specific match number (other columns). An odds ratio equal to 1 indicates that the feature is irrelevant for the classification. We set to 1 all the odds ratios we found to be statistically indistinguishable to 1, using a p-value with a threshold of 0.05. An odds ratio larger than 1 indicates a positive correlation between the feature and a successful outcome. In other words, the feature’s presence raises the success probability. Conversely, an odds ratio smaller than 1 indicates a negative correlation, i.e., the feature’s presence reduces the success probability. The Paradox Move feature is defined using the experts’ survey results. Figure S5 in SI shows the same results for the non-experts case.