Tunneling Quantum Dynamics in Ammonia

Abstract

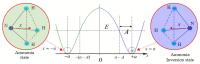
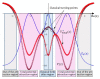
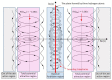
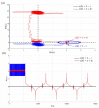
Ammonia is a well-known example of a two-state system and must be described in quantum-mechanical terms. In this article, we will explain the tunneling phenomenon that occurs in ammonia molecules from the perspective of trajectory-based quantum dynamics, rather than the usual quantum probability perspective. The tunneling of the nitrogen atom through the potential barrier in ammonia is not merely a probability problem; there are underlying reasons and mechanisms explaining why and how the tunneling in ammonia can happen. Under the framework of quantum Hamilton mechanics, the tunneling motion of the nitrogen atom in ammonia can be described deterministically in terms of the quantum trajectories of the nitrogen atom and the quantum forces applied. The vibrations of the nitrogen atom about its two equilibrium positions are analyzed in terms of its quantum trajectories, which are solved from the Hamilton equations of motion. The vibration periods are then computed by the quantum trajectories and compared with the experimental measurements.

Keywords: ammonia; quantum Hamilton mechanics; quantum molecular dynamics; quantum trajectory; tunneling dynamics.

Figure 1

The two equilibrium states of the ammonia molecule and their related positions in the double-well potential. The ammonia molecule has the shape of a pyramid, where the three hydrogen atoms form the equilateral triangle and the nitrogen atom is positioned at the apex. The distance of the nitrogen atom to the equilateral triangle plane is denoted by $x$, and the double-well potential is symmetric to $x=0$. The positions $x=\pm a$ are the two equilibrium points of the potential, recognized as the ammonia state and the ammonia inversion state, respectively. The positions $x=\pm \left(a-A\right)$ are the classical turning points, where the nitrogen atom’s kinetic energy is equal to the potential barrier.

Figure 2

The two ground-state wave functions of the nitrogen atom in the double-well potential. (a) ${\Psi }_0^{+}\left(z\right)={\Psi }_{\mathrm{even}}\left(z\right)$ has even symmetry. (b) ${\Psi }_0^{-}\left(z\right)={\Psi }_{\mathrm{odd}}\left(z\right)$ has odd symmetry.

Figure 3

(a) The plots of ${\left|{\psi }_0\left(z\right)\right|}^2$, $V_s\left(z\right)$ and $V_{\mathrm{Total}}\left(z\right)$ for the single-well potential. The parameters are chosen as follows: $B=500{ \mathrm{cm}}^{-1}$, $C=2500{ \mathrm{cm}}^{-1}$, $d=17 \mathrm{pm}$, and $k=2.22$. The maximum point of ${\left|{\psi }_0\left(z\right)\right|}^2$ at $\mathrm{Re}\left(z\right)=-0.1365$ coincides with the minimum point of the potential $V_{\mathrm{Total}}\left(z\right)$, but is different from the minimum point of $V_s\left(z\right)$ at $\mathrm{Re}\left(z\right)=$ $-0.10033$. (b) The complex trajectories of the nitrogen atom solved from (39) show that the equilibrium point $z_{eq}$ is located at the minimum point of the potential $V_{\mathrm{Total}}\left(z\right)$, which is also the point with the maximum probability.

Figure 4

The spatial distributions of the probability density ${\left|{\Psi }_0^{\pm }\left(z\right)\right|}^2$, the double-well potential $V\left(z\right)$, and the total potential $V_{\mathrm{Total}}^{\pm }\left(z\right)$ in the ground state. (a) The maximum point of the probability density ${\left|{\Psi }_0^{+}\left(z\right)\right|}^2$ at $\mathrm{Re}\left(z\right)=\pm 2.08331$ coincides with the minimum point of the total potential $V_{\mathrm{Total}}^{+}\left(z\right)$, but is different from the minimum point of the double-well potential $V\left(z\right)$ at $\mathrm{Re}\left(z\right)=\pm 2.11966$. The probability ${\left|{\Psi }_0^{+}\left(z\right)\right|}^2$ at the origin is ${\left|{\Psi }_0^{+}\left(0\right)\right|}^2=0.001938\ne 0$ which corresponds to the central minimum point of the total potential $V_{\mathrm{Total}}^{+}\left(z\right)$. (b) The probability ${\left|{\Psi }_0^{-}\left(z\right)\right|}^2$ at the origin is zero, corresponding to the infinite total potential $V_{\mathrm{Total}}^{-}\left(z\right)$ at $z=0$.

Figure 5

Three categories of regions in the total potential $V_{\mathrm{Total}}^{+}\left(z\right)$, the double-well potential $V\left(z\right)$, and the nitrogen atom’s kinetic energy $E_k\left(z\right).$ The classical forbidden region is defined by the classical turning points located at $\mathrm{Re}\left(z\right)=\pm 0.468$, where the double-well potential $V\left(z\right)$ is equal to the nitrogen atom’s kinetic energy $E_k\left(z\right).$ The two total-potential attraction regions are centered at the left and right minimum points of the total potential. Outside of the attraction regions, the attraction is too weak to pull the nitrogen atom back to the center of attraction.

Figure 6

Complex trajectories in three types of regions of the nitrogen atom in the ground state. In the classical forbidden region, the closed trajectories are the tunneling trajectories crossing the symmetric plane from one side to the other side. In the total-potential attraction region, the trajectories enclose the equilibrium points at $\mathrm{Re}\left(z\right)=\pm 2.2821$, which are the minimum points of the total potential. The trajectories out of the attraction region are open trajectories.

Figure 7

(a) The plot of the complex trajectories over the surface of the total potential $V_{\mathrm{Total}}^{+}\left(z\right)$, which has a local minimum at $z=0$ and allows the nitrogen atom to pass through. (b) The surface plot of the total potential $V_{\mathrm{Total}}^{-}\left(z\right)$, which goes to infinite at $z=0$ and forbids the nitrogen atom from passing through.

Figure 8

(a) The complex trajectories of the nitrogen atom in the first excited state with $B=500$ and $C=2500$. (b) The spatial distributions of the probability density ${\left|{\Psi }_1^{+}\left(z\right)\right|}^2$, the double-well potential $V\left(z\right)$, and the total potential $V_{\mathrm{Total}}^{+}\left(z\right)$.

Figure 9

The complex trajectories of the nitrogen atom in the states $n=0, 1, 2, 3$ (a–d) with parameters $B=5$ and $C=3000$. The tunneling trajectory ${\mathsf{\Omega }}_5$, which encloses both left and right equilibrium points, appears in the $n=3$ state.

Figure 10

(a) The time evolution of the total potential $V_{\mathrm{Total}}$ shows that around $\mathsf{\tau }=3000$ and $\mathsf{\tau }=6000$ the gap created by the reduction of the potential barrier (marked by the red arrows) forms a tunneling channel, allowing the nitrogen atom to pass through the potential barrier to the other side. (b) The change of the quantum potential $Q$ over time controls the formation of tunneling channels.

Figure 11

The tunneling trajectories launched from different initial positions. The apex of the ammonia state and the ammonia inversion state are, respectively, at $\mathrm{Re}\left(z\right)=-1.775$ and $\mathrm{Re}\left(z\right)=1.73$. The time interval between each apex transition is $∆\tau =1814$, corresponding to the actual time interval $∆t=2.0529\times {10}^{-11}$ s. A complete tunneling period is $∆\tau =3628$, and the tunneling frequency is $24.35 \mathrm{GHz}$.

Figure 12

The tunneling motion in the complex plane with initial positions $z\left(0\right)=2+0i$ (solid red line) and $z\left(0\right)=2-i$ (dash blue line). (a) The trajectory with the initial position $z\left(0\right)=2+0i$ starts to tunnel around $\mathrm{Im}\left(\mathrm{z}\right)=24$, while the trajectory with the initial position $z\left(0\right)=2-i$ has a tunneling trajectory that is more close to the real $z-$axis. (b) As viewed along the real axis, both trajectories start the tunneling process at the same time and have the same tunneling period.

Figure 13

Snapshots of the total potential over the complex plane at several moments. The height of the total potential is labelled by different colors as indicated by the color wheel. The central tunneling channel is stationary in the time interval $0\le \tau \le 4000$ (as (a,b) show). After $\tau =4000$, the channel starts to move to the left-hand side (the black arrows in (c,d) show the moving direction), and reaches the pyramid apex (the ammonia state) at $\tau =4535$ as (e) shows. Then the central tunneling channel changes direction (see the red arrows in (e)) and moves back to the right-hand side of the symmetric plane (refers to (f,g)), meeting the inverted pyramid apex (the ammonia inversion state) at $\tau =6349$ as shown in (h). Then it immediately changes direction (see the red arrows in (h)) and moves back to the left-hand side. (e–h) illustrate a half cycle of the ammonia and ammonia inversion transition. After $\tau =6349$, the tunneling channel moves to the left-hand side in the same process as shown in (f,g). The tunneling channel varies periodically between the two states with associated tunneling trajectory and arrival time, as shown in Figure 11. During the tunneling process, the nitrogen atom rides on the tunneling channel and moves along with it.

Figure 13

Snapshots of the total potential over the complex plane at several moments. The height of the total potential is labelled by different colors as indicated by the color wheel. The central tunneling channel is stationary in the time interval $0\le \tau \le 4000$ (as (a,b) show). After $\tau =4000$, the channel starts to move to the left-hand side (the black arrows in (c,d) show the moving direction), and reaches the pyramid apex (the ammonia state) at $\tau =4535$ as (e) shows. Then the central tunneling channel changes direction (see the red arrows in (e)) and moves back to the right-hand side of the symmetric plane (refers to (f,g)), meeting the inverted pyramid apex (the ammonia inversion state) at $\tau =6349$ as shown in (h). Then it immediately changes direction (see the red arrows in (h)) and moves back to the left-hand side. (e–h) illustrate a half cycle of the ammonia and ammonia inversion transition. After $\tau =6349$, the tunneling channel moves to the left-hand side in the same process as shown in (f,g). The tunneling channel varies periodically between the two states with associated tunneling trajectory and arrival time, as shown in Figure 11. During the tunneling process, the nitrogen atom rides on the tunneling channel and moves along with it.