Dynamic mode decomposition in adaptive mesh refinement and coarsening simulations
- PMID: 34366524
- PMCID: PMC8328142
- DOI: 10.1007/s00366-021-01485-6
Dynamic mode decomposition in adaptive mesh refinement and coarsening simulations
Abstract
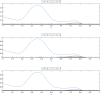
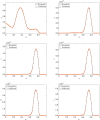
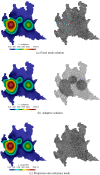
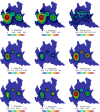
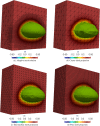
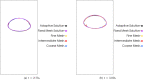
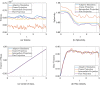
Dynamic mode decomposition (DMD) is a powerful data-driven method used to extract spatio-temporal coherent structures that dictate a given dynamical system. The method consists of stacking collected temporal snapshots into a matrix and mapping the nonlinear dynamics using a linear operator. The classical procedure considers that snapshots possess the same dimensionality for all the observable data. However, this often does not occur in numerical simulations with adaptive mesh refinement/coarsening schemes (AMR/C). This paper proposes a strategy to enable DMD to extract features from observations with different mesh topologies and dimensions, such as those found in AMR/C simulations. For this purpose, the adaptive snapshots are projected onto the same reference function space, enabling the use of snapshot-based methods such as DMD. The present strategy is applied to challenging AMR/C simulations: a continuous diffusion-reaction epidemiological model for COVID-19, a density-driven gravity current simulation, and a bubble rising problem. We also evaluate the DMD efficiency to reconstruct the dynamics and some relevant quantities of interest. In particular, for the SEIRD model and the bubble rising problem, we evaluate DMD's ability to extrapolate in time (short-time future estimates).
Keywords: Adaptive mesh refinement and coarsening; Dimensionality reduction; Dynamic mode decomposition; Mesh projection.
© The Author(s) 2021.
Conflict of interest statement
Conflict of interestThe authors declare that they have no conflict of interest.
Figures






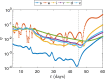

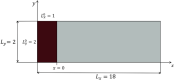



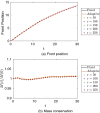
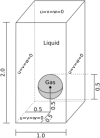


References
-
- Ahmed N, Rebollo TC, John V, Rubino S. A review of variational multiscale methods for the simulation of turbulent incompressible flows. Arch Comput Methods Eng. 2017;24(1):115–164. doi: 10.1007/s11831-015-9161-0. - DOI
-
- Ainsworth M, Oden JT. A posteriori error estimation in finite element analysis. New York: Wiley; 2011.
-
- Alla A, Balzotti C, Briani M, Cristiani E. Understanding mass transfer directions via data-driven models with application to mobile phone data. SIAM J Appl Dyn Syst. 2020;19(2):1372–1391. doi: 10.1137/19M1248479. - DOI
-
- Alnæs MS, Blechta J, Hake J, Johansson A, Kehlet B, Logg A, Richardson C, Ring J, Rognes ME, Wells GN. The Fenics project version 15. Arch Numer Softw. 2015;3:100.
-
- Baddoo PJ, Herrmann B, McKeon BJ, Brunton SL (2021) Kernel learning for robust dynamic mode decomposition: linear and nonlinear disambiguation optimization (LANDO). arXiv:2106.01510 - PMC - PubMed
LinkOut - more resources
Full Text Sources
