Numerical simulation of intracellular drug delivery via rapid squeezing
- PMID: 34367404
- PMCID: PMC8331209
- DOI: 10.1063/5.0059165
Numerical simulation of intracellular drug delivery via rapid squeezing
Abstract
Intracellular drug delivery by rapid squeezing is one of the most recent and simple cell membrane disruption-mediated drug encapsulation approaches. In this method, cell membranes are perforated in a microfluidic setup due to rapid cell deformation during squeezing through constricted channels. While squeezing-based drug loading has been successful in loading drug molecules into various cell types, such as immune cells, cancer cells, and other primary cells, there is so far no comprehensive understanding of the pore opening mechanism on the cell membrane and the systematic analysis on how different channel geometries and squeezing speed influence drug loading. This article aims to develop a three-dimensional computational model to study the intracellular delivery for compound cells squeezing through microfluidic channels. The Lattice Boltzmann method, as the flow solver, integrated with a spring-connected network via frictional coupling, is employed to capture compound capsule dynamics over fast squeezing. The pore size is proportional to the local areal strain of triangular patches on the compound cell through mathematical correlations derived from molecular dynamics and coarse-grained molecular dynamics simulations. We quantify the drug concentration inside the cell cytoplasm by introducing a new mathematical model for passive diffusion after squeezing. Compared to the existing models, the proposed model does not have any empirical parameters that depend on operating conditions and device geometry. Since the compound cell model is new, it is validated by simulating a nucleated cell under a simple shear flow at different capillary numbers and comparing the results with other numerical models reported in literature. The cell deformation during squeezing is also compared with the pattern found from our compound cell squeezing experiment. Afterward, compound cell squeezing is modeled for different cell squeezing velocities, constriction lengths, and constriction widths. We reported the instantaneous cell center velocity, variations of axial and vertical cell dimensions, cell porosity, and normalized drug concentration to shed light on the underlying physics in fast squeezing-based drug delivery. Consistent with experimental findings in the literature, the numerical results confirm that constriction width reduction, constriction length enlargement, and average cell velocity promote intracellular drug delivery. The results show that the existence of the nucleus increases cell porosity and loaded drug concentration after squeezing. Given geometrical parameters and cell average velocity, the maximum porosity is achieved at three different locations: constriction entrance, constriction middle part, and outside the constriction. Our numerical results provide reasonable justifications for experimental findings on the influences of constriction geometry and cell velocity on the performance of cell-squeezing delivery. We expect this model can help design and optimize squeezing-based cargo delivery.
© 2021 Author(s).
Figures




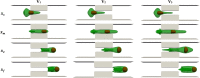






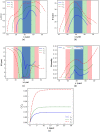
Similar articles
-
Coarse-grained molecular simulation of extracellular vesicle squeezing for drug loading.Phys Chem Chem Phys. 2023 May 3;25(17):12308-12321. doi: 10.1039/d3cp00387f. Phys Chem Chem Phys. 2023. PMID: 37082907 Free PMC article.
-
Multiscale modeling of hemolysis during microfiltration.Microfluid Nanofluidics. 2020 May;24(5):33. doi: 10.1007/s10404-020-02337-3. Epub 2020 Apr 10. Microfluid Nanofluidics. 2020. PMID: 33235552 Free PMC article.
-
Geometrical effects in microfluidic-based microarrays for rapid, efficient single-cell capture of mammalian stem cells and plant cells.Biomicrofluidics. 2012 Jun;6(2):24112-2411217. doi: 10.1063/1.4704521. Epub 2012 Apr 17. Biomicrofluidics. 2012. PMID: 22655021 Free PMC article.
-
Droplet breakup mechanisms in premix membrane emulsification and related microfluidic channels.Adv Colloid Interface Sci. 2021 Apr;290:102393. doi: 10.1016/j.cis.2021.102393. Epub 2021 Mar 2. Adv Colloid Interface Sci. 2021. PMID: 33770649 Review.
-
Microfluidic mechanoporation for cellular delivery and analysis.Mater Today Bio. 2021 Dec 20;13:100193. doi: 10.1016/j.mtbio.2021.100193. eCollection 2022 Jan. Mater Today Bio. 2021. PMID: 35005598 Free PMC article. Review.
Cited by
-
MIML: multiplex image machine learning for high precision cell classification via mechanical traits within microfluidic systems.Microsyst Nanoeng. 2025 Mar 7;11(1):43. doi: 10.1038/s41378-025-00874-x. Microsyst Nanoeng. 2025. PMID: 40050640 Free PMC article.
-
Transient flow-induced deformation of cancer cells in microchannels: a general computational model and experiments.Biomech Model Mechanobiol. 2025 Apr;24(2):489-506. doi: 10.1007/s10237-024-01920-9. Epub 2025 Feb 2. Biomech Model Mechanobiol. 2025. PMID: 39893594 Free PMC article.
-
Could artificial intelligence revolutionize the development of nanovectors for gene therapy and mRNA vaccines?Nano Today. 2022 Dec;47:101665. doi: 10.1016/j.nantod.2022.101665. Epub 2022 Nov 7. Nano Today. 2022. PMID: 37034382 Free PMC article.
-
Coarse-grained molecular simulation of extracellular vesicle squeezing for drug loading.Phys Chem Chem Phys. 2023 May 3;25(17):12308-12321. doi: 10.1039/d3cp00387f. Phys Chem Chem Phys. 2023. PMID: 37082907 Free PMC article.
-
MIML: Multiplex Image Machine Learning for High Precision Cell Classification via Mechanical Traits within Microfluidic Systems.ArXiv [Preprint]. 2025 Feb 24:arXiv:2309.08421v3. ArXiv. 2025. Update in: Microsyst Nanoeng. 2025 Mar 7;11(1):43. doi: 10.1038/s41378-025-00874-x. PMID: 37744465 Free PMC article. Updated. Preprint.
References
-
- Kitao T. and Hattori K., “Erythrocyte entrapment of daunomycin by amphotericin B without hemolysis,” Cancer Res. 40(4), 1351–1353 (1980). - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
