An Energetic Approach to Modeling Cytoskeletal Architecture in Maturing Cardiomyocytes

Abstract

Through a variety of mechanisms, a healthy heart is able to regulate its structure and dynamics across multiple length scales. Disruption of these mechanisms can have a cascading effect, resulting in severe structural and/or functional changes that permeate across different length scales. Due to this hierarchical structure, there is interest in understanding how the components at the various scales coordinate and influence each other. However, much is unknown regarding how myofibril bundles are organized within a densely packed cell and the influence of the subcellular components on the architecture that is formed. To elucidate potential factors influencing cytoskeletal development, we proposed a computational model that integrated interactions at both the cellular and subcellular scale to predict the location of individual myofibril bundles that contributed to the formation of an energetically favorable cytoskeletal network. Our model was tested and validated using experimental metrics derived from analyzing single-cell cardiomyocytes. We demonstrated that our model-generated networks were capable of reproducing the variation observed in experimental cells at different length scales as a result of the stochasticity inherent in the different interactions between the various cellular components. Additionally, we showed that incorporating length-scale parameters resulted in physical constraints that directed cytoskeletal architecture toward a structurally consistent motif. Understanding the mechanisms guiding the formation and organization of the cytoskeleton in individual cardiomyocytes can aid tissue engineers toward developing functional cardiac tissue.

Fig. 1

Schematic overview of major modeling components. Basic model implementation consists of an initialize stage where the cell geometry is predetermined and required parameters are set. The initial distributions of bound and free integrins are determined and the different model components are carried out as outlined in Sec. 3.1.

Fig. 2

Influence of the nucleus on cytoskeletal properties. The nucleus was provided a level of influence on the cytoskeleton corresponding to the energetic cost of creating a curve that passes over the nucleus. This level of influence varied from moderate (a) to major (b) with levels likened to a more elastic or more stiff nucleus, , respectively. The location of the nucleus was altered to mimic the cases where there was no nucleus present (i, Φ), placed in the geometric center position (ii, CP), placed using a horizontal shift of 7 μm left of center (iii, HS) or placed using a vertical shift 7 μm above the center point (iv, VS). The exact placement of the nucleus was fixed at the start of each simulation. The COOP was applied at two different length scales to the networks obtained (v). After performing 6 simulations of each nucleus location in (a) and (b), the average number of curves created over all simulations was recorded (c) as well as the maximum traction stress (d), estimated using the magnitude of the net force at every point in the cell divided by unit cell area. Scale bar: 10 μm.

Fig. 3

Testing length-dependence relationships. Model was implemented on rectangular geometries with aspect ratios varying from 1:1 to 13:1. For each aspect ratio, six simulations were performed and $\alpha$ was set to $\alpha =0$ OFF: absolute-length dependence) or $\alpha =1$ (ON: relative-length dependence). The average number of curves created (a), the average curve length (b), and the average maximum traction stress (c) were computed for each aspect ratio. The shaded region identifies the range of average maximum traction stress values reported from the literature.

Fig. 4

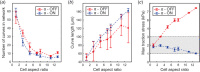
Testing structural consistency. The average COOP was computed at small (∼1 μm) and large (∼15 μm) scales for experimental cells (a) and model-generated networks (b). At each aspect ratio, experimental cells and model simulated networks were combined into a single group and the average COOP was computed (c). The COOP was recorded within each aspect ratio by comparing all possible cell-cell pairs (a, b, c insets). For the 3 μm length scale, networks generated by the model simulations were combined with experimental cells into a single group and the corresponding COOP values (dotted lines) were computed (d). The group containing only experimental data (solid lines) and the group containing only model networks (dashed lines) were also computed for comparison. This was repeated at both the small and large length scales (d, inset). The shaded areas designate the 95% confidence region for the experiment only group. Scale bars: 10 μm. All analysis was performed using previously published experimental data (see Refs. [8,38]) .