Moving Dirac nodes by chemical substitution

Abstract

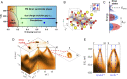
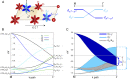
Dirac fermions play a central role in the study of topological phases, for they can generate a variety of exotic states, such as Weyl semimetals and topological insulators. The control and manipulation of Dirac fermions constitute a fundamental step toward the realization of novel concepts of electronic devices and quantum computation. By means of Angle-Resolved Photo-Emission Spectroscopy (ARPES) experiments and ab initio simulations, here, we show that Dirac states can be effectively tuned by doping a transition metal sulfide, [Formula: see text], through Co/Ni substitution. The symmetry and chemical characteristics of this material, combined with the modification of the charge-transfer gap of [Formula: see text] across its phase diagram, lead to the formation of Dirac lines, whose position in k-space can be displaced along the [Formula: see text] symmetry direction and their form reshaped. Not only does the doping x tailor the location and shape of the Dirac bands, but it also controls the metal-insulator transition in the same compound, making [Formula: see text] a model system to functionalize Dirac materials by varying the strength of electron correlations.

Keywords: Dirac semi-metals; correlated electronic systems; functional topological materials.

Fig. 1.

Experimental observation of Dirac states in the phase diagram of ${\mathrm{B}\mathrm{a}\mathrm{C}\mathrm{o}}_{1-x}{\mathrm{N}\mathrm{i}}_x{\mathrm{S}}_2$. (A) Phase diagram of ${\mathrm{B}\mathrm{a}\mathrm{C}\mathrm{o}}_{1-x}{\mathrm{N}\mathrm{i}}_x{\mathrm{S}}_2$. The transition lines between the PM, the paramagnetic insulator (PI), and the antiferromagnetic insulator (AFI) are reported. Colored circles indicate the different doping levels $x$ studied in this work. This doping alters the $d-p$ charge-transfer gap (${\mathrm{\Delta }}_{CT}$). (B) Crystal structure of ${\mathrm{B}\mathrm{a}\mathrm{N}\mathrm{i}\mathrm{S}}_2$. Blue, red, and yellow spheres represent the Ni, S, and Ba atoms, respectively. The tetragonal unit cell is indicated by black solid lines. Lattice parameters are $a$ = 4.44 Å and $c$ = 8.93 Å (45). (B, Upper) Projection of the unit cell in the $xy$ plane, containing two Ni atoms. (C) Schematics of the energy levels. The hybridization of $d-$ and $p-$ orbitals creates the Dirac states, and the $d-p$ charge-transfer gap fixes the position of these states in the $E-k$ space. (D) A three-dimensional ARPES map of ${\mathrm{B}\mathrm{a}\mathrm{N}\mathrm{i}\mathrm{S}}_2$ ($x=1$) taken at 70-eV photon energy. The top surface shows the Fermi surface, and the sides of the cube present the band dispersion along high-symmetry directions. The linearly dispersing bands along $\mathrm{\Gamma }-M$ cross each other at the Fermi level, $E_F$, thus creating four Dirac nodes. (E) We observe the oval-shaped section of the linearly dispersing bands on the $k_x-k_y$ plane for $E-E_F=-100$ meV. The linearly dispersing bands along the major and minor axis of the oval are also shown.

Fig. 2.

Mechanism of band inversion and formation of hybridized Dirac states. (A) Schematics of the $d$- and $p$-orbitals of Ni and S, respectively. (A, Right) The strong hybridization of the $d$-orbitals with the ligand $p$-orbitals, favored by the NSS, is responsible for the band inversion. (B) Band symmetries along the M$\mathrm{\Gamma }$ direction. At the right-hand (left-hand) side, we report the symmetries at $\mathrm{\Gamma }$ (M), while the symmetries in between follow the irreps of the $C_{2v}$ point group, represented by the color code in the key. The outer $+/-$ signs indicate the parity of the respective Bloch wave functions at the beginning and at the end of the $\mathbf{k}$-path. (C) Evolution of the energy splitting between even and odd combinations of $d$-orbitals along M$\mathrm{\Gamma }$. The dominant orbital character is reported. The navy blue (blue) vertical arrows indicate the splitting ${\mathrm{\Delta }}_3$ (${\mathrm{\Delta }}_1$) between the $d_{x^2-y^2}$ ($d_{z^2}$) bands at $\mathrm{\Gamma }$ due to the hybridization with the ligand $p_z$-orbitals. The gray arrow indicates the splitting ${\mathrm{\Delta }}_2$ of $d_{xz}$/$d_{yz}$ bands at $\mathrm{\Gamma }$ due to their hybridization with the $p_x$/$p_y$ orbitals.

Fig. 3.

Experimental ARPES evolution of Dirac states with doping $x$, in ${\text{BaCo}}_{1-x}{\text{Ni}}_x{\text{S}}_2$. (A and B) Dispersion of these states for $x=1$. A shows the iso-energy contours with increasing binding energy. B shows the dispersion along the high-symmetry directions $\mathrm{\Gamma }-M$ and $X-Y$. Note the anisotropy of the dispersion, which is due to the oval shape of the pockets at the Fermi surface. Dashed lines are a guide to the eye that represent schematically the dispersion. Panels C and D and panels E and F are the same as in A and B for the $x=0.75$ and the $x=0.3$ samples, respectively. All spectra are obtained with a photon energy of 70 eV.

Fig. 4.

Evolution of Dirac states with doping x, in ${\mathrm{B}\mathrm{a}\mathrm{C}\mathrm{o}}_{1-x}{\mathrm{N}\mathrm{i}}_x{\mathrm{S}}_2$. (A) Curves fitting the experimental Dirac states for different values of $x$. (B) Evolution of the Dirac states predicted by our HSE/TB calculations of the band structure. (C) Variation of the charge-transfer gap, ${\mathrm{\Delta }}_{\mathrm{C}\mathrm{T}}$, with the Ni content, $x$. The point at $x=0$ is the metastable state adiabatically connected with the metallic phase found for $x>x_{cr}\simeq 0.22$. By reducing $x$ from one to zero, the Dirac point, ${\mathbf{k}}_{\mathrm{D}\mathrm{i}\mathrm{r}\mathrm{a}\mathrm{c}}$, moves toward $\mathrm{\Gamma }$. Correspondingly, the difference between the energy of this point and the Fermi level increases. (D) ${\mathbf{k}}_{\mathrm{D}\mathrm{i}\mathrm{r}\mathrm{a}\mathrm{c}}$ variation for $x=0$ and $x=1$, when we relax the screened-exchange fraction parameter $\alpha$ in the modified HSE functional. The black (red) star is located at the value of $\alpha$ that optimally captures the correlation strength in ${\mathrm{B}\mathrm{a}\mathrm{N}\mathrm{i}\mathrm{S}}_2$ (${\mathrm{B}\mathrm{a}\mathrm{C}\mathrm{o}\mathrm{S}}_2$), used to predict the evolution in B and C. (E) Density of states (DOS) of the $x=0$ collinear SDW solution, as computed by GGA+U (black line) with ab initio values for the local Hubbard repulsion and the modified HSE with values for $\alpha$ covering different correlation strengths. Optimal $\alpha =19\%$ best matches the GGA+U DOS.