SARS-CoV-2 infection in UK university students: lessons from September-December 2020 and modelling insights for future student return

Abstract

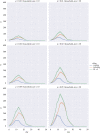
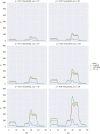
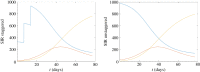
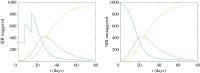
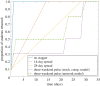
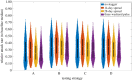
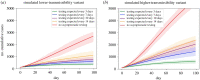
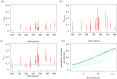
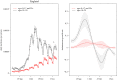
In this paper, we present work on SARS-CoV-2 transmission in UK higher education settings using multiple approaches to assess the extent of university outbreaks, how much those outbreaks may have led to spillover in the community, and the expected effects of control measures. Firstly, we found that the distribution of outbreaks in universities in late 2020 was consistent with the expected importation of infection from arriving students. Considering outbreaks at one university, larger halls of residence posed higher risks for transmission. The dynamics of transmission from university outbreaks to wider communities is complex, and while sometimes spillover does occur, occasionally even large outbreaks do not give any detectable signal of spillover to the local population. Secondly, we explored proposed control measures for reopening and keeping open universities. We found the proposal of staggering the return of students to university residence is of limited value in terms of reducing transmission. We show that student adherence to testing and self-isolation is likely to be much more important for reducing transmission during term time. Finally, we explored strategies for testing students in the context of a more transmissible variant and found that frequent testing would be necessary to prevent a major outbreak.

Keywords: COVID-19; SARS-CoV-2; epidemic modelling; higher education; pandemic modelling.

Figure 1.

Overview of the structure of the article.

Figure 2.

Observed fraction of institutions having an outbreak (*), binned by expected number of incoming cases, and theoretical outbreak probability $\mathcal{P}$ (solid line): for a threshold of 200 cases (a) and 400 cases (b).

Figure 3.

Relative excess of community cases in relation to the reported outbreak sizes across the LTLAs considered in table 4. The sizes of the plot markers scale with the proportion of students attending a university in the same region as their home address. The colours of the markers correspond to the community incidence per 1000 people in each LTLA at the time of peak student-aged cases. These inform the varying levels of community prevalence prior to any student outbreak potentially impacting the community. (a) Cumulative university student outbreak sizes up to 10 days past peak incidence, reported by the UCU. (b) Cumulative university-aged outbreak sizes from 14 days prior to 10 days past peak incidence, reported by PHE.

Figure 4.

Mean cases (represented as dots) per population in MSOAs categorized as high student concentration (black), near high student concentration (red), low student concentration (blue), and far from high student concentration (green) in each of (a) Manchester, (b) Birmingham and (c) Hull. Lines represent the smoothed weekly mean positive cases per population, shaded to cover the 95% confidence intervals of these estimates (details in appendix C).

Figure 5.

Expected number of students in isolation against time for a return spread over 14 days when the probability of a returning student being infected, p, is 0.01 (top row), 0.02 (middle row) and 0.05 (bottom row) for household sizes of 10 individuals (left column) and 20 individuals (right column). Waiting (blue), Isolating (orange), W + I: Waiting + Isolating (green). Bands show 95% interval computed from 100 simulation runs.

Figure 6.

Expected number of students in isolation against time for a return spread over 28 days when the probability of a returning student being infected, p, is 0.01 (top row), 0.02 (middle row) and 0.05 (bottom row) for household sizes of 10 individuals (left column) and 20 individuals (right column). Waiting (blue), Isolating (orange), W + I: Waiting + Isolating (green). Bands show 95% interval computed from 100 simulation runs.

Figure 7.

Expected isolations for a three week pulse return when the probability of a returning student being infected, p, is 0.01 (top row), 0.02 (middle row) and 0.05 (bottom row) for household sizes of 10 individuals (left column) and 20 individuals (right column). Waiting (blue), Isolating (orange), W + I: Waiting + Isolating (green). Bands show 95% interval computed from 100 simulation runs.

Figure 8.

Staggered/unstaggered return temporal profiles. (a) Staggered return (three stages in the first three weeks) in the first three weeks, taking N = 1000 and β = 0.18, p = 0.1, γ = 0.072, with an initial value of R = 2.25. (b) Unstaggered return. In each figure, we show S (blue), I (red) and R (yellow).

Figure 9.

Staggered/unstaggered return temporal profiles. β = 0.18, p = 0.02, initial R = 2.45.

Figure 10.

Staggered/unstaggered return temporal profiles. β = 0.3, p = 0.02, initial R = 4.08.

Figure 11.

Staggered return temporal profiles. We considered four student return patterns: no stagger (blue solid line); return spread over 14 days (orange dashed line); return spread over 28 days (yellow dotted line); three-weekend pulsed return (by course), as used in the stochastic compartmental model (purple dot-dash line); three-weekend pulsed return, as used in the network model (green dot-dash line, cross markers). For this depiction, we present proportion returned with respect to time when assuming 10% of all students were resident in their university accommodation between academic terms.

Figure 12.

Epidemiological outcomes among a student population given differing staggered return strategies to university using a stochastic compartmental model. Outputs are summarized from 10 simulations, with the lines representing the median number of symptomatic and asymptomatic students and the shaded areas showing the 2.5th and 97.5th percentiles. We display distributions corresponding to: (a) no testing of asymptomatics upon student return, (b) all asymptomatics are tested.

Figure 13.

Epidemiological outcomes among a student population given differing staggered return strategies to university compared with a strategy where staggering is not used, using a stochastic compartmental model. Outputs are summarized from 10 simulations, with the continuous lines representing the median number of symptomatic and asymptomatic students and the dashed lines corresponding to the 2.5th and 97.5th percentiles. We display distributions corresponding to: (a) no testing of asymptomatics upon student return, (b) all asymptomatics are tested.

Figure 14.

Epidemiological outcomes among a student population given differing staggered return strategies to university. Outputs summarized from 1000 simulations (with 20 runs per network, for 50 network realizations) for various levels of adherence to NPIs. We considered four strategies: no stagger (blue violin plots); return spread over 14 days (orange violin plots); return spread over 28 days (yellow violin plots); three-weekend pulsed return (purple violin plots). We assumed 100% of adherents engage with return testing. We display distributions corresponding to: (a) relative attack rate, compared with the baseline scenario; (b) time spent in isolation per student; (c) time spent in isolation per adherent student. The white markers denote medians and solid black lines span the 25th to 75th percentiles.

Figure 15.

Temporal profiles of epidemiological measures over the academic term under differing return patterns. Outputs produced from 1000 simulations (with 20 runs per network, for 50 network realizations) for four return patterns: no stagger (blue); return spread over 14 days (orange); return spread over 28 days (yellow); three-weekend pulsed return (purple). Solid lines depict the median profile and shaded regions the 95% prediction interval. Panels from left to right display infection prevalence, cumulative proportion of initial susceptibles infected, and 7-day averaged R, respectively. (a) No return testing; (b) return testing with all adherents participating.

Figure 16.

Relative attack rate distributions under different test before return to study procedures, in combination with strategies for staggered student return. Assumed 90% adhere to isolation, test and trace guidance. For test strategies using two LFTs, the two tests were spaced 3 days apart. We considered four student return patterns: no stagger (blue violin plots); return spread over 14 days (orange violin plots); return spread over 28 days (yellow violin plots); three-weekend pulsed return (purple violin plots). The white markers denote medians and solid black lines span the 25th to 75th percentiles.

Figure 17.

Temporal profiles of cumulative case counts for a simulated population of 15 000 students under differing during-term asymptomatic screening scenarios. We present two scenarios for variant transmissibility: (a) lower-transmissibility variant; (b) higher-transmissibility variant (1.5 times more transmissible than the lower-transmissibility variant). Output produced from 100 runs of each scenario, with a new network generated for each replicate; envelopes show 95% of model runs and solid lines show mean values. Asymptomatic screening scenarios considered are: no asymptomatic testing (red), each person randomly tested with probability 1/14 (yellow), 1/10 (purple), 1/7 (blue), or 1/3 (green) per day, to simulate testing approximately every 14, 10, 7 or 3 days, respectively. Note that this model has many limitations and should be interpreted mainly qualitatively. See main text for a listing of some limitations.

Figure 18.

Results of fitting the model with two levels of mixing to each hall individually, plotted against hall capacity. Circles indicate expected mean and lines 95% confidence intervals. (a) Probability of infection due to global infectious contact. (b) Probability of infection due to household infectious contact. (c) Comparison of the total probability of infection after introduction accounting for household and global infectious contacts compared with the estimated binomial probability of infection given introduction into a household (black dashed line). (d) Comparison of the probability of infection in a household by household size for each hall (blue lines) and the output from the binary regression analysis (black line).

Figure 19.

Growth rate among the student-aged (grey) and community populations (red) across England. University outbreaks are observed on the national scale, with the higher incidence per population among those aged 18–24. The community growth rate in cases increased from late September 2020. However, there was not a statistically significant subsequent increase following the peak in student-aged outbreaks. The shaded regions are the 95% confidence intervals for the relevant quantity.

Figure 20.

Examples of the different types of growth rate patterns observed among student-aged (grey) and community cases (red). The shaded regions are the 95% confidence intervals for the relevant quantity. (a) Bristol, (b) Durham, (c) Leeds and (d) Salford.

Figure 21.

Probabilities of testing positive through time for symptomatic and asymptomatic individuals. We assumed that the probability of positive test results being returned in symptomatic and asymptomatic individuals were equal during the proliferation stage of the virus, but that the probability of asymptomatic individuals testing positive decayed faster in the clearance stage, owing to a shorter mean clearance duration of 6.7 days [53] (a) PCR test; (b) LFT.