Second-Order Disjoint Factor Analysis

Abstract

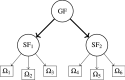
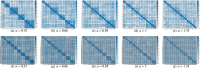
Hierarchical models are often considered to measure latent concepts defining nested sets of manifest variables. Therefore, by supposing a hierarchical relationship among manifest variables, the general latent concept can be represented by a tree structure where each internal node represents a specific order of abstraction for the latent concept measured. In this paper, we propose a new latent factor model called second-order disjoint factor analysis in order to model an unknown hierarchical structure of the manifest variables with two orders. This is a second-order factor analysis, which-respect to the second-order confirmatory factor analysis-is exploratory, nested and estimated simultaneously by maximum likelihood method. Each subset of manifest variables is modeled to be internally consistent and reliable, that is, manifest variables related to a factor measure "consistently" a unique theoretical construct. This feature implies that manifest variables are positively correlated with the related factor and, therefore, the associated factor loadings are constrained to be nonnegative. A cyclic block coordinate descent algorithm is proposed to maximize the likelihood. We present a simulation study that investigates the ability to get reliable factors. Furthermore, the new model is applied to identify the underlying factors of well-being showing the characteristics of the new methodology. A final discussion completes the paper.

Keywords: factor analysis; hierarchical models; latent variable models; reflective models; second-order.

Fig. 1

($50\times 50$) Correlation matrix with a block diagonal structure in four blocks

Fig. 2

Example of second-order disjoint factor model

Fig. 3

Heatmaps of examples of correlation matrix produced by the simulation study with different levels of error. First row: scenario $n=200$, $J=20$, $H=5$; second row: scenario $n=200$, $J=50$, $H=10$