Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Aug 24;118(34):e2104556118.
doi: 10.1073/pnas.2104556118.

Band gaps of crystalline solids from Wannier-localization-based optimal tuning of a screened range-separated hybrid functional

Dahvyd Wing  1 , Guy Ohad  1 , Jonah B Haber  2   3 , Marina R Filip  4 , Stephen E Gant  2   3 , Jeffrey B Neaton  2   3   5 , Leeor Kronik  6
Affiliations

Band gaps of crystalline solids from Wannier-localization-based optimal tuning of a screened range-separated hybrid functional

Dahvyd Wing et al. Proc Natl Acad Sci U S A. .

Abstract

Accurate prediction of fundamental band gaps of crystalline solid-state systems entirely within density functional theory is a long-standing challenge. Here, we present a simple and inexpensive method that achieves this by means of nonempirical optimal tuning of the parameters of a screened range-separated hybrid functional. The tuning involves the enforcement of an ansatz that generalizes the ionization potential theorem to the removal of an electron from an occupied state described by a localized Wannier function in a modestly sized supercell calculation. The method is benchmarked against experiment for a set of systems ranging from narrow band-gap semiconductors to large band-gap insulators, spanning a range of fundamental band gaps from 0.2 to 14.2 electronvolts (eV), and is found to yield quantitative accuracy across the board, with a mean absolute error of ∼0.1 eV and a maximal error of ∼0.2 eV.

Keywords: band gap; density functional theory; optimal tuning.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interest.

Figures

Fig. 1.
Fig. 1.
Illustration of the Wannier-localized, optimal-tuning SRSH approach, for the typical case of AlP. (A) Wavefunction of the valence band maximum (VBM) obtained using the PBE functional. (B) Maximally localized Wannier function used for the optimal tuning procedure. Gray, Al atoms; purple, P atoms. Wavefunction isosurface is shown in blue (positive values) and yellow (negative values) for values of ±5.5×10−4 for the VBM and ±2.8×10−4 for the Wannier function. (C) Deviation from the IP theorem, ΔI, for the SRSH functional, as a function of the range separation parameter, γ, for AlP. (D) The fundamental band gap of AlP, calculated by SRSH, as a function of ΔI. Dashed lines correspond to ΔI = 0.
Fig. 2.
Fig. 2.
Fundamental band gaps predicted by WOT-SRSH, compared to the reference band gaps (fundamental experimental band gaps plus zero-point renormalization energy). The straight line indicates perfect agreement. (Inset) Zoom-in on the 0- to 3-eV region.
See this image and copyright information in PMC

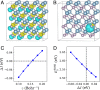
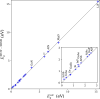
Comment in

  • Advancing solid-state band gap predictions.
    Scuseria GE. Scuseria GE. Proc Natl Acad Sci U S A. 2021 Aug 31;118(35):e2113648118. doi: 10.1073/pnas.2113648118. Proc Natl Acad Sci U S A. 2021. PMID: 34433674 Free PMC article. No abstract available.

References

    1. Kümmel S., Kronik L., Orbital-dependent density functionals: Theory and applications. Rev. Mod. Phys. 80, 3–60 (2008).
    1. Onida G., Reining L., Rubio A., Electronic excitations: Density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 74, 601–659 (2002).
    1. Perdew J. P., Levy M., Physical content of the exact Kohn-Sham orbital energies: Band gaps and derivative discontinuities. Phys. Rev. Lett. 51, 1884–1887 (1983).
    1. Sham L. J., Schlüter M., Density-functional theory of the energy gap. Phys. Rev. Lett. 51, 1888–1891 (1983).
    1. Perdew J. P., Parr R. G., Levy M., Balduz J. L., Density-functional theory for fractional particle number: Derivative discontinuities of the energy. Phys. Rev. Lett. 49, 1691–1694 (1982).

Publication types