Not straightforward: modelling non-linearity in training load and injury research

Abstract

Objectives: To determine whether the relationship between training load and injury risk is non-linear and investigate ways of handling non-linearity.

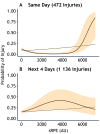
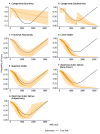
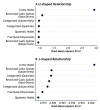
Methods: We analysed daily training load and injury data from three cohorts: Norwegian elite U-19 football (n=81, 55% male, mean age 17 years (SD 1)), Norwegian Premier League football (n=36, 100% male, mean age 26 years (SD 4)) and elite youth handball (n=205, 36% male, mean age 17 years (SD 1)). The relationship between session rating of perceived exertion (sRPE) and probability of injury was estimated with restricted cubic splines in mixed-effects logistic regression models. Simulations were carried out to compare the ability of seven methods to model non-linear relationships, using visualisations, root-mean-squared error and coverage of prediction intervals as performance metrics.

Results: No relationships were identified in the football cohorts; however, a J-shaped relationship was found between sRPE and the probability of injury on the same day for elite youth handball players (p<0.001). In the simulations, the only methods capable of non-linear modelling relationships were the quadratic model, fractional polynomials and restricted cubic splines.

Conclusion: The relationship between training load and injury risk should be assumed to be non-linear. Future research should apply appropriate methods to account for non-linearity, such as fractional polynomials or restricted cubic splines. We propose a guide for which method(s) to use in a range of different situations.

Keywords: injury; methodological; statistics; training.

Figure 1

Illustration of time periods for calculating (A) daily ACWR 7:21-period and (B) micro-cycle ACWR 1:3-period. The first day that ACWR is calculated from is denoted day 0. The space between two tick marks represent 1 day (24 hours). For B, a microcycle period consists of all activity before a new match (M). That is, recovery days after the previous match as well as the training days before the next match. Days denoted with negative numbers are training days before the next match (M-1: being the day before the match; M-2: 2 days before a match and so on). Days with positive numbers are recovery and training days after a match (M+1: being the day after a match, M+2: 2 days after a match). The number of days between matches varies by the match schedule. How a team plan their training and recovery activities varies and is dependent on the teams’ philosophy. For A, injury on the same day is defined as an injury on day 0, and future injury is defined as an injury occurring during the next 4 days excluding day 0. For B, future injury was defined as an injury occurring during the next microcycle excluding day 0. ACWR, acute:chronic workload ratio.

Figure 2

Probability of injury in elite youth handball on (A) the sameday and (B) the next 4 days, for each level of session rating of perceived exertion (sRPE) measured in arbitrary units (AU), as predicted by mixed effects logistic regression models with restricted cubic splines. The predictions pertain to a 17-year-old female. The yellow area represents 95% cluster-robust CIs around predicted values. The straight line shows the same predictions from an equivalent model without splines (ie, assuming linearity). For figure part B, modelling the response of injury in the next 4 days, multiple injuries on the same day were considered one event and an injury event would pertain to four load values and are therefore included four times.

Figure 3

Probability of injury for each level of session rating of perceived exertion (sRPE) as predicted by seven different methods of modelling load. The yellow line represents the ability of the method to capture the U-shaped relationship (shown by the black line). The yellow area corresponds to the prediction interval. The predictions are based on 8494 sRPE values sampled from a highly skewed distribution in a Norwegian elite U-19 football dataset.

Figure 4

The mean root-mean-squared error (RMSE) of 1900 permutations for seven different methods modelling a non-linear (A) U-shaped relationship between session rating of perceived exertion (sRPE) and probability of injury, and (B) J-shaped relationship between acute:chronic workload ratio (ACWR) and probability of injury. The methods are arranged from top-to-bottom by the method with highest RMSE (most error) to the method with lowest RMSE. Thus, the best methods (those with lowest RMSE) are arranged towards the bottom. For figure part A, fractional polynomials and restricted cubic splines (subjectively) were the best methods, while for figure part B, fractional polynomials and the quadratic model were the best methods. The calculations are based on a Norwegian elite U-19 football dataset with 8494 sRPE values for (A) U shape and 6308 ACWR values for (B) J shape. RMSE cannot be compared between the two shapes, only within each shape.