A Model for Tacit Communication in Collaborative Human-UAV Search-and-Rescue

Abstract

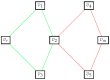
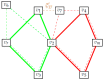
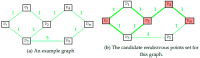
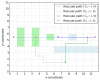
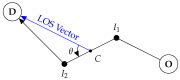
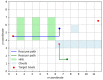
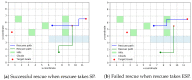
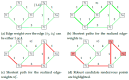
Tacit communication can be exploited in human robot interaction (HRI) scenarios to achieve desirable outcomes. This paper models a particular search and rescue (SAR) scenario as a modified asymmetric rendezvous game, where limited signaling capabilities are present between the two players-rescuer and rescuee. We model our situation as a co-operative Stackelberg signaling game, where the rescuer acts as a leader in signaling its intent to the rescuee. We present an efficient game-theoretic approach to obtain the optimal signaling policy to be employed by the rescuer. We then robustify this approach to uncertainties in the rescue topology and deviations in rescuee behavior. The paper thus introduces a game-theoretic framework to model an HRI scenario with implicit communication capacity.

Keywords: game theory; human robot interaction; signaling.

Figure A1

A possible representation of ${\mathcal{G}}^1$. All edge weights are minimum. ${\widehat{\mathcal{X}}}^1$ would contain $\{v_r,v_2,v_m\}$. $v_2$ here connects the two sub-graphs red and green.

Figure A2

A possible representation of ${\mathcal{G}}^k$. All thick edge weights are maximum and all thin edges are minimum weight. ${\widehat{\mathcal{X}}}^k$ would contain $\{v_r,v_2,v_m\}$. $v_2$ here connects the two sub-graphs red and green. The dashed lines indicate edges in ${\mathcal{G}}^{*k}$ sub-graph. We want to show that ${\xi }_{17}^{\prime }$ cannot exist for any edge-weights $\left\{w_{ij}^{k^{\prime }}\right\}$.

Figure 1

Rescue area topology. Rescuee takes optimal path (blue) to the indicated target. The rescuer picks an optimal rendezvous point (red cross) to meet the rescuee. Clouds (blue shading) act as obstacles to the UAV and hills (green shading) act as obstacles to the rescuee.

Figure 2

Illustration of candidate rendezvous set. As an illustrative example on obtaining the candidate rendezvous set, consider the graph in (a). For the given edge-weights, we have two shortest paths from v_r to v_m, one alongv_r − v₁ − v₂ − v₄ − v_m and one along v_r − v₃ − v₂ − v₄ − v_m. The set of points that lie on every shortest path is highlighted in red in (b). Thus for this graph ${\mathcal{X}}_m$ = {v_r,v₂,v₄,v_m}.

Figure 3

Optimal signal switching with velocity change. Rendezvous trajectories when $k_v=1.6$ and $k_v=1.9$.

Figure 4

Illustration of LOS (Line-of-Sight) vector from a path segment. In VBN, the cost of traversing the path segment $I_1{I}_2$ depends not just on the edge-weight along this edge, but also the angle $\theta$ made by the segment with the LOS vector from the mid-point C of the segment to the destination.

Figure 5

Strips layout $K_{los}=1$. For the rescuee, the green shaded cells have a cost-to-traverse randomly sampled from $[2.5,3]$ and all other cells have a cost-to-traverse picked from $[1,1.5]$. The topology faced by the rescuee in going left resembles a parallel range of hills with valleys between them and we will name this general layout ‘strips’ for convenience in referring to. The rescuer planned to meet in the grid-square $(6,3)$. Here a grid square is denoted by co-ordinates of bottom left corner.

Figure 6

Scatter Layout. For the rescuee, the green shaded cells have a cost-to-traverse randomly sampled from [2.5, 3] and all other cells have a cost-to-traverse picked from [1, 1.5]. We label this terrain topology as ‘scatter’ layout as the ‘hills’ are scattered around. The rescuer planned to rendezvous at (9, 5).

Figure 7

Illustration of robust candidate rendezvous set. (a) shows the graph in consideration. We see that the edge weights over all edges except one are constants. (b,c) show the shortest paths over the graph for two different realizations of edge-weights. (d) highlights the set of robust candidate rendezvous points. So we have ${\mathcal{X}}_m$ = {v_r,v₄,v_m}.

Figure 8

Robust optimal signaling policy in a simulated run. Clouds (blue shading) act as ‘high edge weight’ regions to the UAV and hills (green shading) act as ‘high edge weight’ regions to the rescuee. The optimal signal sent out was indicating the right target goal.

Figure 9

Conservativeness of the robust policy. The dark green hilly regions have a cost-to-traverse of 3 for the rescuee. Each white grid square has a cost to traverse of 1, while in the second figure the light green shaded grid squares have a cost to traverse of 1.5.

Figure 10

Comparative run of the robust and stochastic signaling policies. Over the same topographical layout we observe that the optimal signal to be sent changes with the robustness criteria we choose. In (a), the rescuer employs the completely robust signaling policy and incurs a worst case cost-of-rescue of 19.5. In (b) the rescuer incurs a worst case cost-of-rescue of 13. Here, we take K = 50 samples and 1 − γ = 0.9 as the threshold for admitting a node into the stochastic candidate rendezvous set.