Micro Satellite Orbital Boost by Electrodynamic Tethers
- PMID: 34442538
- PMCID: PMC8400572
- DOI: 10.3390/mi12080916
Micro Satellite Orbital Boost by Electrodynamic Tethers
Abstract
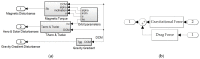
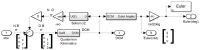
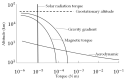
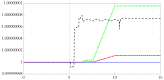
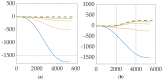
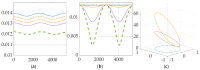
In this manuscript, a method for maneuvering a spacecraft using electrically charged tethers is explored. The spacecraft's velocity vector can be modified by interacting with Earth's magnetic field. Through this method, a spacecraft can maintain an orbit indefinitely by reboosting without the constraint of limited propellant. The spacecraft-tether system dynamics in low Earth orbit are simulated to evaluate the effects of Lorentz force and torques on translational motion. With 500-meter tethers charged with a 1-amp current, a 100-kg spacecraft can gain 250 m of altitude in one orbit. By evaluating the combined effects of Lorenz force and the coupled effects of Lorentz torque propagation through Euler's moment equation and Newton's translational motion equations, the simulated spacecraft-tether system can orbit indefinitely at altitudes as low as 275 km. Through a rare evaluation of the nonlinear coupling of the six differential equations of motion, the one finding is that an electrodynamic tether can be used to maintain a spacecraft's orbit height indefinitely for very low Earth orbits. However, the reboost maneuver is inefficient for high inclination orbits and has high electrical power requirement. To overcome greater aerodynamic drag at lower altitudes, longer tethers with higher power draw are required.
Keywords: actuators; aerodynamic drag; and control; cubesats; dynamics; guidance; magnetic field; mini/micro satellites; navigation; orbital dynamics; spacecraft maneuvering; tether.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
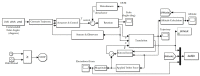
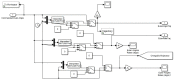

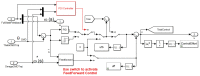
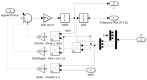




References
-
- Garcia M. Space Debris and Human Spacecraft. NASA Space Station Articles. [(accessed on 31 May 2021)];2021 Available online: https://www.nasa.gov/mission_pages/station/news/orbital_debris.html.
-
- Ecuador Pegasus Satellite Fears over Space Debris Crash. BBC News Website, 24 May 2013. [(accessed on 31 May 2021)]; Available online: https://www.bbc.com/news/world-latin-america-22635671.
-
- Foust J. ESA Spacecraft Dodges Potential Collision with Starlink Satellite. Space News. 2 September 2019. [(accessed on 31 May 2021)]; Available online: https://spacenews.com/esa-spacecraft-dodges-potential-collision-with-sta...
-
- Bedrossian N., Bhatt S., Kang W., Ross I.M. Zero propellant maneuver guidance. IEEE Control. Syst. Mag. 2009;29:53–73.
-
- Wie B. Singularity analysis and visualization for single-gimbal Control Moment Gyros System. J. Guid. Control Dyn. 2004;30:272–282. doi: 10.2514/1.9167. - DOI
LinkOut - more resources
Full Text Sources

