From signal-based to comprehensive magnetic resonance imaging

Abstract

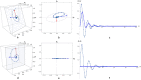
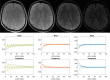
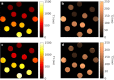
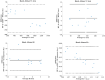
We present and evaluate a new insight into magnetic resonance imaging (MRI). It is based on the algebraic description of the magnetization during the transient response-including intrinsic magnetic resonance parameters such as longitudinal and transverse relaxation times (T₁, T₂) and proton density (PD) and experimental conditions such as radiofrequency field (B₁) and constant/homogeneous magnetic field (B₀) from associated scanners. We exploit the correspondence among three different elements: the signal evolution as a result of a repetitive sequence of blocks of radiofrequency excitation pulses and encoding gradients, the continuous Bloch equations and the mathematical description of a sequence as a linear system. This approach simultaneously provides, in a single measurement, all quantitative parameters of interest as well as associated system imperfections. Finally, we demonstrate the in-vivo applicability of the new concept on a clinical MRI scanner.

Figure 1

(a) Illustration of the “propagator”: a single block of events. μ is the input–output magnetization, in red the RF excitations and in blue the gradients. (b) A typical train of blocks in a MR pulse sequence. We will use identical blocks or operators A = A₁ = A₂ = … = A_n.

Figure 2

(a–c) The repeated block consists of an excitation with flip angle $\alpha$=30º, $\mathrm{\beta }$=14º (accumulated phase as a result of off-resonance during ${\mathrm{T}}_{\mathrm{R}}$,${\mathrm{T}}_{\mathrm{R}}$ =10 ms), relaxation times are ${\mathrm{T}}_1$= 878 ms, ${\mathrm{T}}_2$= 47.5 ms. ${\mathbf{n}}_1$ and ${\mathbf{n}}_2$ span the plane of oscillation. The magnetization vector always points to a point of this plane. Only the orientation of the plane is fixed throughout the evolution; it shifts parallel to ${\mathbf{n}}_3$. Figure (a) 3D trajectory, (b) x–y projection (transversal plane), (c) x and y component (signals measured in quadrature). Figures (d–f) similar to (a–c) with on-resonance ($\mathrm{\beta }$=0º). The plane spanned b. ${\mathbf{n}}_1$ and ${\mathbf{n}}_2$ is the x–z plane throughout the entire evolution. The points represent the magnetization difference vector and its evolution along the sequence. The continuous line is the corresponding continuously parametrized $\mathbf{y}\left(\mathrm{\tau }\right)={\mathbf{A}}^{\mathrm{\tau }/{\mathrm{T}}_{\mathrm{R}}}{\mathbf{\mu }}_0$ . The quantity $\mathbf{y}\left(\mathrm{\tau }\right)$ satisfies the differential equation: $\frac{\mathrm{d}}{\mathrm{dt}}\mathbf{y}\left(\mathrm{t}\right)=\mathbf{B}·\mathbf{y}\left(\mathrm{t}\right)$ with $\exp \left(\mathbf{B}\right)={\mathbf{A}}^{1/{\mathrm{T}}_{\mathrm{R}}}$. $\mathbf{y}\left(\mathrm{\tau }\right)$ is not the fully continuous trajectory of the magnetization $\mathrm{\mu }$. However, $\mathbf{y}\left(\mathrm{\tau }\right)$ and $\mathrm{\mu }$ are equal at the discrete time points: $\mathbf{y}\left(\mathrm{\tau },=,\mathrm{n},{\mathrm{T}}_{\mathrm{R}}\right)={\mathrm{\mu }}_{\mathrm{n}}$ .

Figure 3

(a)${\mathrm{T}}_2-\mathrm{\beta }$ species: parameter space, (b–e) are the eigenvalue maps on the complex plane where three eigenvalues belong to each parameter species: red and blue are the complex eigenvalues, green represents the real eigenvalue. Eigenvalues of the repeated ${\alpha }_{\mathrm{x}}$ propagator are shown in (b). The ${\alpha }_{\mathrm{x}}-{\alpha }_{\mathrm{y}}$ propagator with excitation flip angle $\alpha ={30}^{\circ }$ is shown in (c), and in (d) “${\alpha }_{\mathrm{x}}-{\alpha }_{\mathrm{x}+\mathrm{\delta }}$ ” scheme with $\alpha ={150}^{\circ }$ and $\mathrm{\delta }={75}^{\circ }$. The eigenvalue space for ${\alpha }_{\mathrm{x}}-{\mathrm{\gamma }}_{\mathrm{y}}-{\alpha }_{\mathrm{y}}-{\mathrm{\gamma }}_{\mathrm{x}}$ with $\alpha ={30}^{\circ }$ and $\mathrm{\gamma }={175}^{\circ }$ is shown in (e). For all maps ${\mathrm{T}}_1$=878 ms and ${\mathrm{T}}_{\mathrm{R}}$=12 ms. In (c) one eigenvalue point belongs to the two $\mathrm{\beta }$ and $\mathrm{\beta }+{180}^{\circ }$ species.

Figure 4

Images in the first row show the transient contrast at time points 1, 3, 5, 7 along the acquisition in a balanced pulse sequence in a “${\alpha }_{\mathrm{x}}$ scheme”. The second row shows for this sequence the signal as it evolves along the echo train for three voxels (depicted on the anatomical image). The left and right subfigures shows are from the blue and green voxels, where the spins are on-resonance. The middle subfigure (red voxel) shows a spiral in the complex signal plane. This clearly shows the regularity of the evolution. On the right subfigure middle and bottom the orthogonal real and imaginary components are depicted. The frequency of the oscillations is constant, the decay of the amplitudes is exponential. The steady state is not zero. The fitted curves show the fitted harmonic oscillator model.

Figure 5

The first row shows the transient contrast at different time points along the acquisition in a balanced pulse sequence for the propagator as a composite of pulses according to the “${\alpha }_{\mathrm{x}}-{\mathrm{\gamma }}_{\mathrm{y}}-{\alpha }_{\mathrm{y}}-{\mathrm{\gamma }}_{\mathrm{x}}$ ” MP-b-nSSFP scheme. The second and third rows show the signal and fit for three highlighted voxels from three different tissues. The observations of the four different echoes in each block of the propagator is shown with different symbols (., + , $\times$,*).

Figure 6

The first row shows the maps from the proposed balanced pulse sequence for the propagator as a composite of pulses according to the “${\alpha }_{\mathrm{x}}-{\mathrm{\gamma }}_{\mathrm{y}}-{\alpha }_{\mathrm{y}}-{\mathrm{\gamma }}_{\mathrm{x}}$ ” MP-b-nSSFP scheme ($\alpha =90;\mathrm{\gamma }=175)$. The second row show maps obtained using conventional MAGIC. (a,c) T1 maps. (b,d) T2 maps.

Figure 7

Bland–Altman plots comparing ROI mean ${\mathrm{T}}_1$ and ${\mathrm{T}}_2$ values of the proposed MP-b-nSSFP sequence with the “${\alpha }_{\mathrm{x}}-{\mathrm{\gamma }}_{\mathrm{y}}-{\alpha }_{\mathrm{y}}-{\mathrm{\gamma }}_{\mathrm{x}}$ ” scheme ($\alpha =90;\mathrm{\gamma }=175)$ and MAGIC.

Figure 8

The parametric maps derived with the proposed model are shown estimated from the MP-b-nSSFP sequence with α = 30º, γ = 175º, TR = 30 ms. Top row shows: (a) PD (proton density, a.u.); (b) ${\mathrm{T}}_1$(ms); (c) ${\mathrm{T}}_2$ (ms); (d) ${\mathrm{B}}_1^{+}$ (excitation RF field scaling factor); (e)${\mathrm{B}}_0$ (deviation in static magnetic field; Hz); (f) ${\mathrm{\rho }}^2\mathrm{\eta }=\det \left(\mathrm{A}\right)={\mathrm{\epsilon }}_2^2{\mathrm{\epsilon }}_1$ (HO harmonic oscillator), (g) synthetic T₁-weighted; (h) synthetic T₂-weighted; (i) synthetic T₂-FLAIR.

Figure 9

The parametric maps and synthetic images as obtained with MAGIC : (a) PD (proton density, a.u.); (b) ${\mathrm{T}}_1$(ms); (c) ${\mathrm{T}}_2$ (ms); (d) synthetic T₁-weighted; (e) synthetic T₂-weighted; (f) synthetic T₂-FLAIR.