Nonprehensile Manipulation of Parts on a Horizontal Circularly Oscillating Platform with Dynamic Dry Friction Control

Abstract

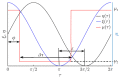
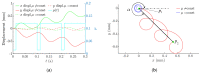
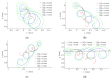
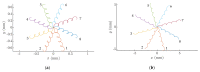
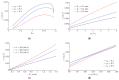
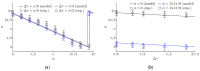
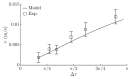
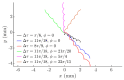
This paper presents a novel method for nonprehensile manipulation of parts on a circularly oscillating platform when the effective coefficient of dry friction between the part and the platform is being dynamically controlled. Theoretical and experimental analyses have been performed to validate the proposed method and to determine the control parameters that define the characteristics of the part's motion. A mathematical model of the manipulation process with dynamic dry friction control was developed and solved. The modeling showed that by changing the phase shift between the function for dynamic dry friction control and the function defining the circular motion of the platform, the part can be moved in any direction as the angle of displacement can be controlled in a full range from 0 to 2π. The nature of the trajectory and the mean displacement velocity of the part mainly depend on the width of the rectangular function for dynamic dry friction control. To verify the theoretical findings, an experimental setup was developed, and experiments of manipulation were carried out. The experimental results qualitatively confirmed the theoretical findings. The presented analysis enriches the classical theories of nonprehensile manipulation on oscillating platforms, and the presented findings are relevant for mechatronics, robotics, mechanics, electronics, medical, and other industries.

Keywords: dry friction; nonprehensile manipulation; oscillating platform; planar motion; vibration and control.

Figure 1

Dynamic model of nonprehensile manipulation on a circularly oscillating platform with dry friction control: (1) part; (2) platform; (3) piezoelectric actuator.

Figure 2

Principle of dry friction control in respect of the period of the function defining the circular motion of the platform.

Figure 3

Displacement of the part when µ₁ = 0.122, µ₂ = µ₁/8, g = 9.81 m/s², A_e = 0.31 mm, ω = 62.8 rad/s, ε = π/2, ϕ = 0, Δτ = π/4: (a) displacement vs. time and the effective dry friction coefficient vs. time; (b) motion trajectory of the part and the angle of displacement α.

Figure 4

Trajectories of the part when µ₁ = 0.122, µ₂ = µ₁/8, g = 9.81 m/s², ω = 62.8 rad/s, ε = π/2; (1) A_e = 0.28 mm, (2) A_e = 0.31 mm, and (3) A_e = 0.32 mm; (a) ϕ = 0, Δτ = π/10; (b) ϕ = 0, Δτ = π/4; (c) ϕ = 11π/9, Δτ = π/4; and (d) ϕ = 17π/9, Δτ = π/4.

Figure 5

Trajectories of the part at different values of the phase shift ϕ when µ₁ = 0.12, µ₂ = µ₁/8, g = 9.81 m/s², A_e = 0.28 mm, ω = 62.8 rad/s, ε = π/2, (1), ϕ = 0, (2), ϕ = π/4; (3), ϕ = π/2; (4), ϕ = 3π/4; (5), ϕ = π; (6), ϕ = 5π/4; (7), ϕ = 3π/2; (8), ϕ = 7π/4: (a) as Δτ = π/6; (b) as Δτ = π.

Figure 6

Mean displacement velocity depending on: (a) Δτ when µ₂ = µ₁/8, g = 9.81 m/s², A_e = 0.28 mm, ω = 62.8 rad/s, ε = π/2, ϕ = 0; (b) µ₁/µ₂ when µ₁ = 0.1, g = 9.81 m/s², ω = 62.8 rad/s, ε = π/2, ϕ = 0, Δτ = π/6; (c) circular excitation amplitude A_e when µ₁ = 0.1, µ₂ = µ₁/8, g = 9.81 m/s², ε = π/2, ϕ = π/2, Δτ = 2π/3; (d) circular excitation frequency ω when µ₂ = µ₁/8, g = 9.81 m/s², ε = π/2, A_e = 0.28 mm, ϕ = π/2, Δτ = 2π/3.

Figure 7

The displacement angle α depending on: (a) phase shift ϕ when µ₁ = 0.1, µ₂ = µ₁/8, g = 9.81 m/s², A_e = 0.28 mm, ω = 62.8 rad/s, ε = π/2; (b) Δτ when µ₂ = µ₁/8, g = 9.81 m/s², A_e = 0.28 mm, ω = 62.8 rad/s, ε = π/2; (c) excitation amplitude A_e when µ₁ = 0.1, µ₂ = µ₁/8, g = 9.81 m/s², ε =π/2, ϕ = π/2, Δτ = 2π/3; (d) excitation frequency ω when µ₂ = µ₁/8, g = 9.81 m/s², ε = π/2, A_e = 0.28 mm, ϕ = π/2, Δτ = 2π/3.

Figure 8

Experimental setup for manipulation of parts on a horizontal circularly oscillating platform with dynamic dry friction control: (a) scheme where (1) part to be manipulated; (2) platform; (3) elastic rods; (4) piezoelectric actuator; (5) electric motor; (6) eccentric mechanism; (7) electric motor power supply; (8) optical reference sensor, (9) vibration analyzer; (10) arbitrary waveform generator; (11) high frequency vibration amplifier; (12) digital oscilloscope; (13) video camera; (14) computer; (b) general view of the platform for nonprehensile manipulation with dry friction control.

Figure 9

Experimental and modeling results of α depending on: (a) the phase shift ϕ when µ₁ = 0.1, µ₂ = µ₁/8, g = 9.81 m/s², A_e = 0.28 mm, ω = 62.8 rad/s, ε = π/2; (b) Δτ when µ₁ = 0.1, µ₂ = µ₁/8, g = 9.81 m/s², A_e = 0.28 mm, ω = 62.8 rad/s, ε = π/2.

Figure 10

Experimental and modeling results of the mean displacement velocity depending on Δτ when µ₁ = 0.1, µ₂ = µ₁/8, g = 9.81 m/s², A_e = 0.28 mm, ω = 62.8 rad/s, ε = π/2, ϕ = 0.

Figure 11

Captured experimental trajectories of the part when A_e = 0.28 mm, ω = 62.8 rad/s, ε = π/2.