Machine-Learning-Assisted Free Energy Simulation of Solution-Phase and Enzyme Reactions
- PMID: 34468138
- PMCID: PMC9070000
- DOI: 10.1021/acs.jctc.1c00565
Machine-Learning-Assisted Free Energy Simulation of Solution-Phase and Enzyme Reactions
Abstract
Despite recent advances in the development of machine learning potentials (MLPs) for biomolecular simulations, there has been limited effort on developing stable and accurate MLPs for enzymatic reactions. Here we report a protocol for performing machine-learning-assisted free energy simulation of solution-phase and enzyme reactions at the ab initio quantum-mechanical/molecular-mechanical (ai-QM/MM) level of accuracy. Within our protocol, the MLP is built to reproduce the ai-QM/MM energy and forces on both QM (reactive) and MM (solvent/enzyme) atoms. As an alternative strategy, a delta machine learning potential (ΔMLP) is trained to reproduce the differences between the ai-QM/MM and semiempirical (se) QM/MM energies and forces. To account for the effect of the condensed-phase environment in both MLP and ΔMLP, the DeePMD representation of a molecular system is extended to incorporate the external electrostatic potential and field on each QM atom. Using the Menshutkin and chorismate mutase reactions as examples, we show that the developed MLP and ΔMLP reproduce the ai-QM/MM energy and forces with errors that on average are less than 1.0 kcal/mol and 1.0 kcal mol-1 Å-1, respectively, for representative configurations along the reaction pathway. For both reactions, MLP/ΔMLP-based simulations yielded free energy profiles that differed by less than 1.0 kcal/mol from the reference ai-QM/MM results at only a fraction of the computational cost.
Figures

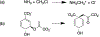






References
-
- Warshel A Computer Simulations of Enzyme Catalysis: Methods, Progress, and Insights. Ann. Rev. Biophys. Biomol. Struct 2003, 32, 425–443. - PubMed
-
- Lin H; Truhlar DG QM/MM: What Have We Learned, Where Are We, and Where Do We Go From Here? Theor. Chem. Acc 2007, 117, 185–199.
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
