Constrained Mixture Models of Soft Tissue Growth and Remodeling - Twenty Years After

Abstract

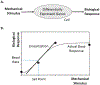
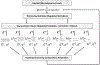
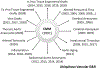
Soft biological tissues compromise diverse cell types and extracellular matrix constituents, each of which can possess individual natural configurations, material properties, and rates of turnover. For this reason, mixture-based models of growth (changes in mass) and remodeling (change in microstructure) are well-suited for studying tissue adaptations, disease progression, and responses to injury or clinical intervention. Such approaches also can be used to design improved tissue engineered constructs to repair, replace, or regenerate tissues. Focusing on blood vessels as archetypes of soft tissues, this paper reviews a constrained mixture theory introduced twenty years ago and explores its usage since by contrasting simulations of diverse vascular conditions. The discussion is framed within the concept of mechanical homeostasis, with consideration of solid-fluid interactions, inflammation, and cell signaling highlighting both past accomplishments and future opportunities as we seek to understand better the evolving composition, geometry, and material behaviors of soft tissues under complex conditions.

Keywords: artery; homeostasis; mechanobiology; thrombus; tissue engineering; vein.

Figure 1.

Schema of finite deformations associated with growth and remodeling (G&R) of a soft tissue in maturity using a constrained mixture model. Individual constituents α = 1,2, …, N are assumed to be deposited within extant matrix at preferred deposition stretches G^α(τ) at G&R time τ ∈ [0, s], each relative to individual evolving natural (stress-free) configurations ${\kappa }_n^{\alpha }(\tau )$. Thereafter, these constituents may deform further because they are constrained to move with the tissue, the in vivo configuration of which evolves from κ(τ) at time τ to κ(s) at time s. 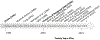Note that the reference configuration κ(0) for the tissue need not be stress-free or traction-free; indeed an in vivo configuration such as that near mean arterial pressure is often convenient in vascular mechanics. Finally, it is the constituent-specific deformation ${\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(s\right)=\mathbf{F}\left(s\right){\mathbf{F}}^{-1}\left(\tau \right){\mathbf{G}}^{\alpha }\left(\tau \right)$ that is most important because the associated constituent-specific stored energy function depends on this deformation alone. Of course, at the time of deposition, ${\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(\tau \right)\equiv {\mathbf{G}}^{\alpha }\left(\tau \right)$.

Figure 2.

A. Schema of a mechanobiological response: a mechanical stimulus drives differential gene expression, leading to different gene products that define the biological response. B. Typical sigmoidal biological response to a mechanical stimulus, as, for example, production of eNOS by endothelial cells in response to increased wall shear stress or production of collagen by smooth muscle cells or fibroblasts in response to increased intramural stress. Importantly, this nonlinear, saturating response can be approximated linearly for changes about the homeostatic set-point, which is often sufficient if the biological response is fast enough to prevent stresses from deviating too much from homeostatic.

Figure 3.

Schema of negative feedback characteristic of mechanical homeostasis in blood vessels and associated modeling via a constrained mixture model of N constituents. For illustrative purposes, constituent N=1 is assumed to not degrade during the G&R period of interest, as, for example elastic fibers under normal conditions in maturity. Importantly, the other constituents are deposited at a rate modulated by gain K^α > 0 and they degrade at rate k^α > 0, noting that deposition is at a homeostatic prestretch G^α >1 and particular orientation defined by angle α^α.

Figure 4.

Chronological summary of implementations of the same constrained mixture model (CMM) by one group to study vascular adaptations, diseases, and interventions. That one basic theoretical framework, enriched with condition-specific constitutive relations for mass production, removal, and constituent properties, can describe such diverse situations provides some confidence in the general utility of the approach.

Figure 5.

Simple timeline showing some key advances in modeling G&R, emphasizing in particular the seminal paper of Skalak in 1981, the introduction of a general constrained mixture theory twenty years after (submitted 2001, published 2002), and yet unimagined opportunities (?) again twenty years thereafter. Notwithstanding the importance of the theory of finite volumetric growth – formalized by Rodriguez and colleagues in 1994 and quickly shown to be useful by Taber, Rachev, and others – consistent with the review herein this timeline focuses primarily on key advances for the constrained mixture model (CMM), including the first finite element implementations in 2005/2006, fluid-solid-growth modeling first used in 2007 but advanced generally in 2009, the utility of such models in describing tissue engineered constructs (introduced in 2009, advanced in 2014, shown to be useful for scaffold design in 2015, and used to guide a clinical trial in 2020), the concept of mechanobiological stability introduced in 2014 and extended in 2019, and finally the computational efficiency engendered by the assumption of quasi-static mechanobiological equilibria shown in 2020 as well as the importance of coupling across scales, including with cell signaling models to appear in 2021. Note, too, some of the key reviews and books that address broader approaches to G&R.