Imaging in thick samples, a phased Monte Carlo radiation transfer algorithm
- PMID: 34490761
- PMCID: PMC8421375
- DOI: 10.1117/1.JBO.26.9.096004
Imaging in thick samples, a phased Monte Carlo radiation transfer algorithm
Abstract
Significance: Optical microscopy is characterized by the ability to get high resolution, below 1 μm, high contrast, functional and quantitative images. The use of shaped illumination, such as with lightsheet microscopy, has led to greater three-dimensional isotropic resolution with low phototoxicity. However, in most complex samples and tissues, optical imaging is limited by scattering. Many solutions to this issue have been proposed, from using passive approaches such as Bessel beam illumination to active methods incorporating aberration correction, but making fair comparisons between different approaches has proven to be challenging.
Aim: We present a phase-encoded Monte Carlo radiation transfer algorithm (φMC) capable of comparing the merits of different illumination strategies or predicting the performance of an individual approach.
Approach: We show that φMC is capable of modeling interference phenomena such as Gaussian or Bessel beams and compare the model with experiment.
Results: Using this verified model, we show that, for a sample with homogeneously distributed scatterers, there is no inherent advantage to illuminating a sample with a conical wave (Bessel beam) instead of a spherical wave (Gaussian beam), except for maintaining a greater depth of focus.
Conclusion: φMC is adaptable to any illumination geometry, sample property, or beam type (such as fractal or layered scatterer distribution) and as such provides a powerful predictive tool for optical imaging in thick samples.
Keywords: Bessel; Monte Carlo methods; light scattering; phase; photons; scattering.
Figures
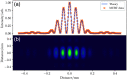
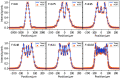
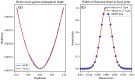

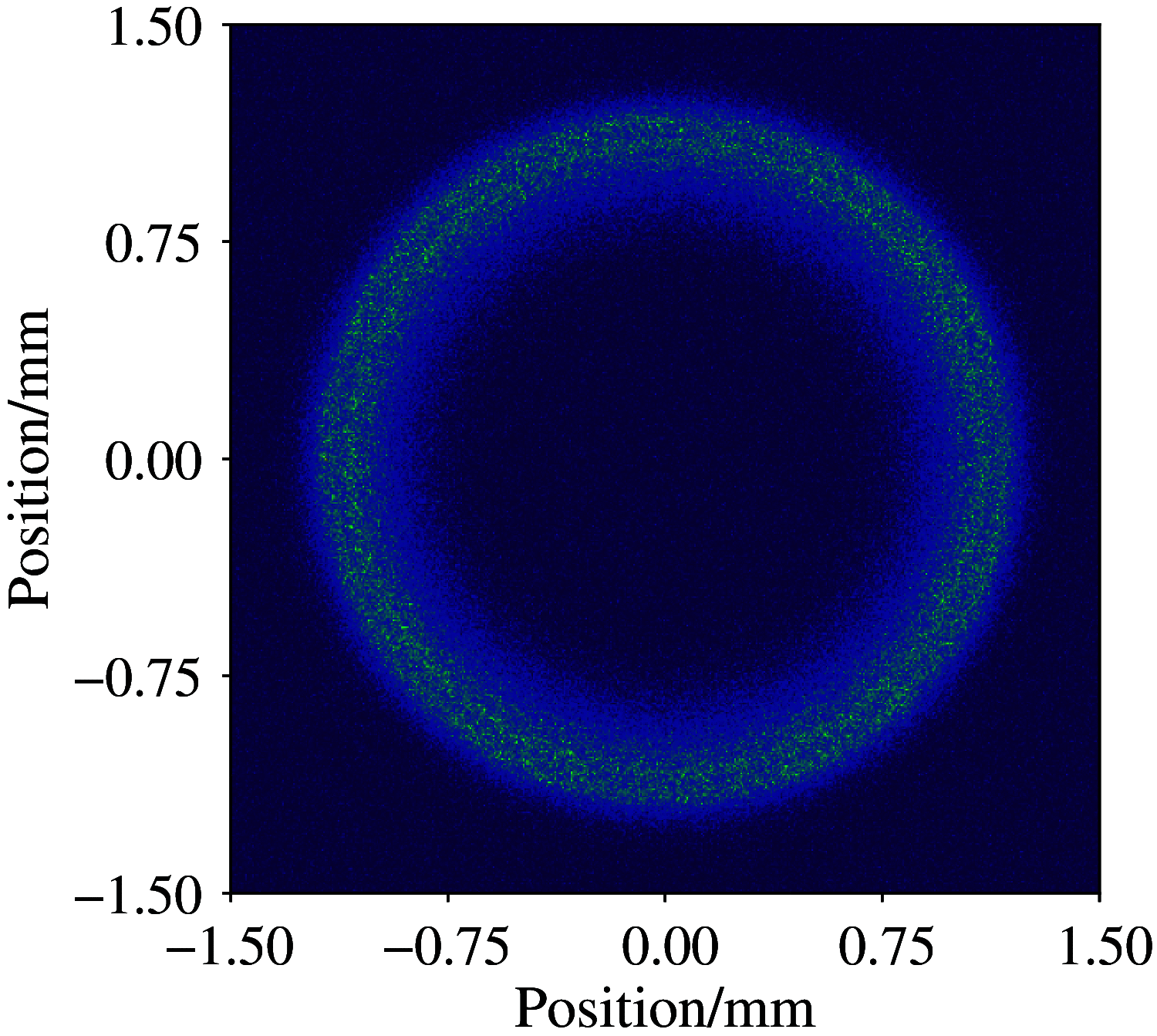



References
-
- Wood K., Reynolds R., “A model for the scattered light contribution and polarization of the diffuse Hα galactic background,” Astrophys. J. 525(2), 799 (1999).ASJOAB10.1086/307939 - DOI

