An integrated framework for building trustworthy data-driven epidemiological models: Application to the COVID-19 outbreak in New York City

Abstract

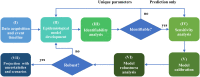
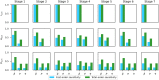
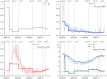
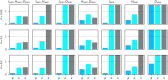
Epidemiological models can provide the dynamic evolution of a pandemic but they are based on many assumptions and parameters that have to be adjusted over the time the pandemic lasts. However, often the available data are not sufficient to identify the model parameters and hence infer the unobserved dynamics. Here, we develop a general framework for building a trustworthy data-driven epidemiological model, consisting of a workflow that integrates data acquisition and event timeline, model development, identifiability analysis, sensitivity analysis, model calibration, model robustness analysis, and projection with uncertainties in different scenarios. In particular, we apply this framework to propose a modified susceptible-exposed-infectious-recovered (SEIR) model, including new compartments and model vaccination in order to project the transmission dynamics of COVID-19 in New York City (NYC). We find that we can uniquely estimate the model parameters and accurately project the daily new infection cases, hospitalizations, and deaths, in agreement with the available data from NYC's government's website. In addition, we employ the calibrated data-driven model to study the effects of vaccination and timing of reopening indoor dining in NYC.

Fig 1. A general framework for building a trustworthy data-driven epidemiological model—An overview of the main contribution.

In this work, we propose a general framework for building a trustworthy data-driven epidemiological model, which constructs a workflow to integrate data acquisition and event timeline, model development, identifiability analysis, sensitivity analysis, model calibration, model robustness analysis, and projection with uncertainties and scenarios. We first introduce a modified SEIR model that accommodates the pandemic data in New York City. Secondly, we study the structural identifiability, practical identifiability, and sensitivity to examine the relationship between the model’s data and parameters. We then calibrate the identifiable model parameters using simulated annealing and MCMC simulation. Model robustness is then checked to study how the model behaves under random perturbations. In addition, we demonstrate the model’s projective capabilities with uncertainties. Finally, reopening scenarios are investigated as a reference for policymakers.

Fig 2. COVID-19 epidemic in New York City: Data and event timeline.

(a) Daily confirmed cases (February 29, 2020–February 4, 2021). A person is classified as a confirmed COVID-19 case when they test positive in a molecular test (PCR). We split the data into seven time periods based on interventions implemented. The starting times of interventions are shown on the top of each subfigure. (b) Daily hospitalized population (February 29, 2020–February 4, 2021). (c) Daily deceased population. (February 29, 2020–February 4, 2021). A deceased individual is classified as a disease-related death if they had a positive PCR test for the virus within the last 60 days. (d) Daily vaccinated population. (December 14, 2020–February 4, 2021).

Fig 3. Transition diagram between epidemiological classes.

We modify the classic SEIR model to include presymptomatic (P), asymptomatic (A), hospitalized (H), isolated (Q), and deceased (D) individuals. The given data are the inflows of symptomatic (I), hospitalized (H), and deceased (D) individuals. The parameters to estimate are (β, p, q). See Table 1 for the notations and the initial values. See Table 2 for the parameters. See Eq (1) for the corresponding ODE system.

Fig 4. The procedure of choosing parameters to fit.

(a) The procedure of determining parameters to fit. We fix d_E, d_P, d_I, d_A, d_H, d_Q because they are biologically determined, and then fix ϵ, δ due to the result from the correlation matrix analysis. (b) The correlation matrix of five parameters. Each colored off-diagonal cell represents the correlation between two parameters. Green means (almost) not statistically correlated while yellow/purple represents positively/negatively correlated, respectively.

Fig 5. Sensitivity of each quantity of interest (I_sum, H_sum,D_sum) with respect to each parameter (β, p, q).

The parameter β is the most important parameter for all three quantities of interest in every stage of the pandemic. The parameter p has no influence on I_sum. The parameter q has no influence on I_sum or H_sum.

Fig 6. Estimation of daily cases, hospitalizations, deaths, and vaccinations in New York City.

(a) Estimation of daily cases. (b) Estimation of daily hospitalizations. (c) Estimation of daily deaths. (d) We calculate the number of effective vaccinations as a weighted sum of the number of first and second doses administered as shown in Fig 2; we approximate the daily number of effective vaccinations linearly and assume it grows linearly until it reaches the maximum capacity of 20,000 per day.

Fig 7. Estimation of the unobserved dynamics in all the model compartments (S,E, P, I, A, H, Q, D, R).

The number of susceptible individuals (S) drops significantly as the number of cases hikes after December 2020.

Fig 8. Estimation of parameters and reproduction numbers.

(a) Estimated time-dependent transmission rate β(t). (b) Estimated time-dependent hospitalization ratio p(t), compared with daily hospitalizations over daily cases calculated from the raw data. (c) Estimated time-dependent death from hospital ratio q(t), compared with daily deaths over daily hospitalizations calculated from the raw data. (d) Estimated control reproduction number ${\mathcal{R}}_c$ and effective reproduction number ${\mathcal{R}}_e$ calculated by the estimated parameters, compared with 1/2 of the logarithm of daily cases.

Fig 9. Average Relative Error (ARE) of (β, p, q) in different observable settings.

Each row corresponds to a standard deviation level of random noise multiplied to the observables. Each column represents an observable setting. When (I_sum, H_sum, D_sum) or (H_sum, D_sum) are given, ARE is lower than the threshold 1. Therefore, our model is robust to noise in the NYC dataset. In the rest of of the missing observable cases, our model would not be robust to perturbations, which is consistent with the structural identifiability result.

Fig 10. Projection of daily cases, hospitalizations, and deaths in New York City with uncertainties and scenarios.

Reopening scenarios on February 14 and March 14 are considered. An increase in infectious, hospitalized, and deceased population is expected if the restaurants are reopened in the same way as Stage 5 (September 30, 2020 to December 14, 2020). Postponing the reopening of restaurants from February 14 to March 14 may reduce the number of infectious, hospitalized, and deceased individuals. The actual situation might vary depending on the details and implementations of the actual indoor dining policies that take place in 2021. Remarks: The projections were made and the paper was submitted in February. When updating the paper in June, we overlaid the new data of daily cases, hospitalizations, and deaths from February to June as the testing data. Indoor dining was actually reopened on February 14.