Generation of multicellular spatiotemporal models of population dynamics from ordinary differential equations, with applications in viral infection

Abstract

Background: The biophysics of an organism span multiple scales from subcellular to organismal and include processes characterized by spatial properties, such as the diffusion of molecules, cell migration, and flow of intravenous fluids. Mathematical biology seeks to explain biophysical processes in mathematical terms at, and across, all relevant spatial and temporal scales, through the generation of representative models. While non-spatial, ordinary differential equation (ODE) models are often used and readily calibrated to experimental data, they do not explicitly represent the spatial and stochastic features of a biological system, limiting their insights and applications. However, spatial models describing biological systems with spatial information are mathematically complex and computationally expensive, which limits the ability to calibrate and deploy them and highlights the need for simpler methods able to model the spatial features of biological systems.

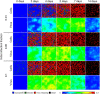
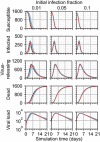
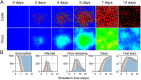
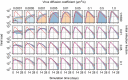
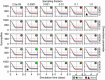
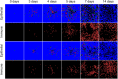
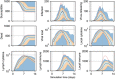
Results: In this work, we develop a formal method for deriving cell-based, spatial, multicellular models from ODE models of population dynamics in biological systems, and vice versa. We provide examples of generating spatiotemporal, multicellular models from ODE models of viral infection and immune response. In these models, the determinants of agreement of spatial and non-spatial models are the degree of spatial heterogeneity in viral production and rates of extracellular viral diffusion and decay. We show how ODE model parameters can implicitly represent spatial parameters, and cell-based spatial models can generate uncertain predictions through sensitivity to stochastic cellular events, which is not a feature of ODE models. Using our method, we can test ODE models in a multicellular, spatial context and translate information to and from non-spatial and spatial models, which help to employ spatiotemporal multicellular models using calibrated ODE model parameters. We additionally investigate objects and processes implicitly represented by ODE model terms and parameters and improve the reproducibility of spatial, stochastic models.

Conclusion: We developed and demonstrate a method for generating spatiotemporal, multicellular models from non-spatial population dynamics models of multicellular systems. We envision employing our method to generate new ODE model terms from spatiotemporal and multicellular models, recast popular ODE models on a cellular basis, and generate better models for critical applications where spatial and stochastic features affect outcomes.

Keywords: Agent-based modeling; Multicellular systems; Multiscale modeling.

Fig. 1

Spatial model results of viral infection in a two-dimensional, epithelial sheet. Results shown for 1% (top), 5% (middle), and 10% (bottom) initially infected cells at 0, 3, 4, 5, 7, and 14 days in simulation time. Epithelial cells shown as blue when susceptible, green when infected, red when virus-releasing, and black when dead. Lower-right color bar shows levels in the virus field, from blue (0) to red (0.2)

Fig. 2

Scalar results from 100 replicas of the spatial model of viral infection. Results shown for 1% (left), 5% (center), and 10% (right) initially infected cells. Medians shown as black lines. 0th to 100th quantiles shaded as blue, 10th to 90th as orange, and 25th to 75th as light blue. ODE model results shown as red dashed lines

Fig. 3

Spatial and ODE model results of viral infection in a two-dimensional, epithelial sheet with one initially infected cell. A Spatial model results of one simulation replica at 0, 3, 4, 5, 7, and 14 days in simulation time. Epithelial cells and extracellular virus shown as in Fig. 1. B Scalar results from 100 replicas of the spatial model. Medians shown as black lines. 0th to 100th quantiles shaded as blue, 10th to 90th as orange, and 25th to 75th as light blue. ODE model results shown as red dashed lines

Fig. 4

Infection model results while varying spatial model parameters. A Number of susceptible cells from 100 replicas of the spatial model of viral infection while varying initial infection fraction and virus diffusion coefficient. Medians shown as black lines. 0th to 100th quantiles shaded as blue, 10th to 90th as orange, and 25th to 75th as light blue. ODE model results shown as red dashed lines. ODE model results with best-fit infectivity shown as magenta dotted lines. B Efficiency of infectivity (top), measured as the ratio of fitted to original ODE model infectivity, and score of fit (bottom), measured as the mean of the NMAE for all variables of the fitted ODE model, for all spatial model parameter variations. Results for efficiency of infectivity are shaded from lowest value (red) to highest value (green), and for score of fit from zero (green) to one (red)

Fig. 5

Viral load from 100 replicas of the spatial model of viral infection while varying initial infection fraction and virus diffusion coefficient. Medians shown as black lines. 0th to 100th quantiles shaded as blue, 10th to 90th as orange, and 25th to 75th as light blue. ODE model results shown as red dashed lines. ODE model results with best-fit infectivity shown as magenta dotted lines

Fig. 6

Spatial model results of viral infection and immune response in a quasi-two-dimensional, epithelial sheet. Results shown for 1% (top), 5% (middle), and 10% (bottom) initially infected cells at 0, 2, 3, 4, 7, and 14 days in simulation time. Epithelial cells shown as in Fig. 1. Immune cells shown as dark red. Lower-right color bar shows levels in the virus and cytokine fields, from blue (0) to red (0.05)

Fig. 7

Scalar results from 100 replicas of the spatial model of viral infection and immune response. Results shown for 1% (left), 5% (center), and 10% (right) initially infected cells. Medians shown as black lines. 0th to 100th quantiles shaded as blue, 10th to 90th as orange, and 25th to 75th as light blue. ODE model results shown as red dashed lines

Fig. 8

Susceptible cells from 100 replicas of the spatial model of viral infection while varying immune cell sampling fraction and chemotaxis parameter. Medians shown as black lines. 0th to 100th quantiles shaded as blue, 10th to 90th as orange, and 25th to 75th as light blue. ODE model results shown as red dashed lines. Star marks best. Triangle marks worst. Circles with green to red shading show best to worst total error, respectively

Fig. 9

Viral load from 100 replicas of the spatial model of viral infection while varying immune cell sampling fraction and chemotaxis parameter. Medians shown as black lines. 0th to 100th quantiles shaded as blue, 10th to 90th as orange, and 25th to 75th as light blue. ODE model results shown as red dashed lines. Star marks best. Triangle marks worst. Circles with green to red shading show best to worst total error, respectively

Fig. 10

Spatial model results from two simulation replicas of viral infection and immune response in a quasi-two-dimensional, epithelial sheet with best-fit immune response parameters and one initially infected cell. Results shown at 0, 3, 4, 5, 7 and 14 days in simulation time. Epithelial and immune cells shown as in Fig. 6

Fig. 11

Scalar results from 100 replicas of the spatial model of viral infection and immune response with best-fit immune response parameters and one initially infected cell. Medians shown as black lines. 0th to 100th quantiles shaded as blue, 10th to 90th as orange, and 25th to 75th as light blue. ODE model results shown as red dashed lines