Field-tunable toroidal moment in a chiral-lattice magnet

Abstract

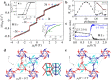
Ferrotoroidal order, which represents a spontaneous arrangement of toroidal moments, has recently been found in a few linear magnetoelectric materials. However, tuning toroidal moments in these materials is challenging. Here, we report switching between ferritoroidal and ferrotoroidal phases by a small magnetic field, in a chiral triangular-lattice magnet BaCoSiO₄ with tri-spin vortices. Upon applying a magnetic field, we observe multi-stair metamagnetic transitions, characterized by equidistant steps in the net magnetic and toroidal moments. This highly unusual ferri-ferroic order appears to come as a result of an unusual hierarchy of frustrated isotropic exchange couplings revealed by first principle calculations, and the antisymmetric exchange interactions driven by the structural chirality. In contrast to the previously known toroidal materials identified via a linear magnetoelectric effect, BaCoSiO₄ is a qualitatively new multiferroic with an unusual coupling between several different orders, and opens up new avenues for realizing easily tunable toroidal orders.

Fig. 1. Toroidal moment and magnetic chirality of spin vortex configurations with 3-fold rotation symmetry.

Four chiral noncoplanar structures are divided into groups of two left-handed ones and two right-handed ones. Those within each group are connected by 2-fold rotations and those between two groups by a mirror operation. The spins (axial vector) are represented as arrows. The dashed line with an ellipsoid indicates one of the three 2-fold axes. Three relevant physical quantities are defined with spins {S_i = 1, 2, 3} numbered anticlockwise: toroidal moment t = ∑_ir_i × S_i, where r_i is the vector from the center of the triangle to spin S_i; vector chirality ϵ = S₁ × S₂ + S₂ × S₃ + S₃ × S₁; scalar chirality κ = (S₁ × S₂) ⋅ S₃. Green symbols + and − for a toroidal moment and vector chirality denote the direction of these quantities with respect to the net magnetic moment, + for parallel and − for antiparallel. The magnetic vector chirality characterizes the sense of spin rotation along an oriented loop (or line), while the toroidal moment is associated with that around a center. Scalar spin chirality is a measure of non-coplanarity that does not necessarily have a sense of rotation. In the current example, toroidal moment and scalar chirality have a one-to-one correspondence to the net magnetic moment for a given handedness, since all of them are odd under time reversal. In a crystalline material with these chiral spin trimers as basic units, a ferro alignment of net magnetic moments of trimers will lead to a ferro ordering of toroidal moments and scalar chirality.

Fig. 2. Zero-field magnetic structure and field-induced ferri- to ferrotoroidal transition in BaCoSiO₄.

a The isothermal bulk magnetization data (open circles) measured at 2 K with the field parallel to the c-axis and the theoretical calculations (red line) from the full spin Hamiltonian, showing a good agreement between data and calculations. The magnetization up to 60 T in a pulsed magnetic field at 1.5 K is shown in the lower inset, and the magnetization hysteresis at low fields in the upper inset. See caption of panel (d) for the meaning of symbols + and −. b The refined agreement factor for the powder neutron diffraction data as a function of uniform rotation in the ab plane. The dashed line marks the best refinement. Inset shows the integrated intensity of the magnetic reflection (2/3 2/3 0) as a function of temperature with an order parameter fit $~{\left(1-T/T_{\mathrm{N}}\right)}^{2\beta }$ (solid line), where β is the critical exponent. The error bars are used to show the standard deviation given by the square root of the number of neutron counts. c The integrated intensities of reflection (2/3 2/3 0) and (−1 1 0) as a function of the magnetic field with H∥c at 1.5 K. d Zero-field magnetic structure of BaCoSiO₄ in a $\sqrt{3}\times \sqrt{3}$ supercell solved from powder neutron diffraction data, showing three interpenetrating ferrotoroidal sublattices (red, blue, and cyan) formed by the dominant exchange interactions J_t (intralayer) and J_z (interlayer). The direction of the toroidal moment for each sublattice is denoted + if it is parallel to the c-axis and − if antiparallel. The red and blue sublattices have the same toroidal moment, while the cyan has the opposite moment, leading to a ferritoroidal state with a total moment +1t. The primitive crystallographic unit cell is indicated by the dotted lines. e Magnetic structure of BaCoSiO₄ at 2 T solved from single-crystal neutron diffraction data. All spins on the cyan sublattice are reversed, leading to a ferrotoroidal state with a total toroidal moment +3t. Triangles in panels (d, e) lie in two adjacent layers, which are bridged by the interlayer interaction J_z.

Fig. 3. Microscopic magnetic model and the underlying mechanism for the ferritoroidal to ferrotoroidal transition.

a Magnetic exchange pathways of BaCoSiO₄, showing three intralayer couplings $\left\{J_t,J_t^{\prime },J_t^{{}^{″}}\right\}$ and two interlayer couplings {J_z, J_c}. Three components of a DM vector on the nearest-neighbor J_t bonds are indicated by red arrows in a local reference frame. b Density functional theory calculation of exchange interaction strengths as a function of onsite interaction U. The dashed line marks the set of couplings with U = 4.41 eV that matches the Weiss temperature from the magnetic susceptibility (Table S2). c Minimal energy configurations for three spins {S_i, i = 1, 2, 3} on a triangle with an antiferromagnetic Heisenberg interaction and an in-plane DM interaction. The DM vectors {D_i, i = 1, 2, 3} (green arrows) are related by 3-fold rotation symmetry and have the same sense of rotation as the tilting of apical oxygens shown in panel (a). Each vector makes an ~30° angle with the bond, see main text for details. For this set of DM vectors, the resulting spin structure (pink arrows) generates a toroidal moment t (black arrows) that is always parallel to the magnetization M. d Energy balance between the ferri- to ferrotoroidal state in magnetic fields. The “frustrated” triangular units that do not have 120° configurations (and cost more energy) are highlighted in pink for both states. The ferrotoroidal state has less colored triangles in the ab plane; therefore, it is energetically favored by the interactions $\left\{J_t^{\prime },J_t^{{}^{″}}\right\}$, similarly the ferritoroidal state is favored by the interaction J_c. Competition between these subleading interactions results in the ferritoroidal structure with a lower energy in zero field. The transition to the ferrotoroidal state occurs when the energy difference is compensated by the Zeeman energy in magnetic fields.