Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Sep 9;11(1):17948.
doi: 10.1038/s41598-021-97222-6.

Flow estimation solely from image data through persistent homology analysis

Anna Suzuki  1 , Miyuki Miyazawa  2 , James M Minto  3 , Takeshi Tsuji  4   5 , Ippei Obayashi  6 , Yasuaki Hiraoka  7 , Takatoshi Ito  2
Affiliations

Flow estimation solely from image data through persistent homology analysis

Anna Suzuki et al. Sci Rep. .

Abstract

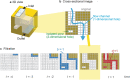
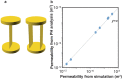
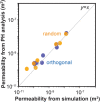
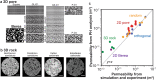
Topological data analysis is an emerging concept of data analysis for characterizing shapes. A state-of-the-art tool in topological data analysis is persistent homology, which is expected to summarize quantified topological and geometric features. Although persistent homology is useful for revealing the topological and geometric information, it is difficult to interpret the parameters of persistent homology themselves and difficult to directly relate the parameters to physical properties. In this study, we focus on connectivity and apertures of flow channels detected from persistent homology analysis. We propose a method to estimate permeability in fracture networks from parameters of persistent homology. Synthetic 3D fracture network patterns and their direct flow simulations are used for the validation. The results suggest that the persistent homology can estimate fluid flow in fracture network based on the image data. This method can easily derive the flow phenomena based on the information of the structure.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

Figure 1
Figure 1
Persistent homology analysis for fracture networks by HomCloud. (a) 3D view and (b) cross-sectional image of fracture network with a flow channel (light blue arrow) and an isolated pore (shown as green). (c) Schematic of filtration process. White grids express void spaces. Blue grids are the grids that were removed during the current thinning iteration. Red grids are the grids that were added during the thickening process.
Figure 2
Figure 2
Detecting flow channels using inverted images (a) ring-shaped, internal void-structure that is not connected to the outside, and (b) its inverted image. (c) ring-shaped, internal void-structure with two channels that is connected to the outside and forms a flow channel. (d) Its inverted image. The left column shows 3D view of images. The center column describes processes of filtration. The right column lists Betti numbers b1.
Figure 3
Figure 3
Fractured models. (a) Outside and (b) inside of model. (c) Orthogonal distribution and (d) random distribution of fracture networks.
Figure 4
Figure 4
Estimation of fracture apertures by persistent homology (PH) analysis. (a) Orthogonal fracture networks and (b) random fracture networks.
Figure 5
Figure 5
Validation with simple models. (a) One or two fracture penetrating the model. The top and bottom are the inlet and the outlet. (b) Comparison of permeability between persistent homology (PH) analysis and direct simulation. The calculated permeability is listed in Table 2.
Figure 6
Figure 6
Estimation of permeability by persistent homology (PH) analysis for orthogonal fracture networks (blue) and random fracture networks (orange). The calculated permeability is listed in Table 1.
Figure 7
Figure 7
Streamlines (green lines) in fracture network simulated in OpenFOAM.
Figure 8
Figure 8
Estimation of permeability by persistent homology (PH) analysis. (a) 2D images from Mehmani and Hamdi, (b) 3D rock images from Andrew et al., and (c) comparison with direct simulation and experiment. The values are listed in Table 3.
Figure 9
Figure 9
Simulation in OpenFOAM. (a) Fracture network with upper and lower boundaries. (b) Discretized model.
See this image and copyright information in PMC

References

    1. Renard P, de Marsily G. Calculating equivalent permeability: A review. Adv. Water Resour. 1997;20:253–278. doi: 10.1016/S0309-1708(96)00050-4. - DOI
    1. Costa A. Permeability-porosity relationship: A reexamination of the Kozeny–Carman equation based on a fractal pore-space geometry assumption. Geophys. Res. Lett. 2006;33:1–5. doi: 10.1029/2005GL025134. - DOI
    1. Carman PC. Fluid flow through granular beds. Trans. Chem. Eng. 1937;15:S32–S48.
    1. Zimmerman RW, Bodvarsson GS. Effective transmissivity of two-dimensional fracture networks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996;33:433–438. doi: 10.1016/0148-9062(95)00067-4. - DOI
    1. Snow D. Anisotropic permeability of fractured media. Water Resour. Res. 1969;5:1273–1289. doi: 10.1029/WR005i006p01273. - DOI